Az algoritmusok tervezése során igen gyakran találkozunk a legkisebb vagy a legnagyobb elem kiválasztásának feladatával. Az sem ritka, hogy az ezektől eltérő sorszámú k-adik elemet kell megkeresnünk. Ebben a fejezetben a kiválasztások feladatát nézzük meg közelebbről, és nem csak megoldó algoritmusokat adunk – köztük egy véletlenített eljárást is –, hanem néhány alsó korlátot is bizonyítunk a lehetséges megoldások lépésszámára.
Ebben a fejezetben X legyen egy megszámlálható számosságú halmaz, melyen adott a ≤ teljes rendezés: reflexív, antiszimmetrikus, tranzitív és bármely két elem összehasonlítható. (Példáinkban X az egész számok halmaza lesz a szokásos rendezéssel.) Használjuk még az x<y jelölést arra az esetre, amikor x≤y és x≠y; ez egy úgynevezett erős rendezés. Jelölje X* az X-ből képzett véges sorozatok halmazát.
Definíció: Egy u∈X*-beli sorozat növekvően rendezett, ha 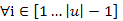 esetén (ui ≤ ui+1). Hasonlóan definiálhatjuk a csökkenően rendezett sorozat fogalmát is.
esetén (ui ≤ ui+1). Hasonlóan definiálhatjuk a csökkenően rendezett sorozat fogalmát is.
Megjegyzés. A továbbiakban rendezettség alatt mindig a növekvő rendezettséget értjük.
Definíció: Legyen u∈X* tetszőleges sorozat és 1≤k≤|u| tetszőleges egész. Az x∈X elemet az u sorozat k–adik elemének hívjuk, ha megegyezik az u rendezettjének k-adik elemével. Ha k=1 akkor minimális, ha k=|u| maximális elemről, ha 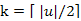 , akkor mediánról beszélünk.
, akkor mediánról beszélünk.
Például az u=31,45,13,24,7,12,8 sorozat minimuma 7, maximuma 45 és a mediánja 13 (a rendezett sorozat 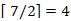 indexű eleme).
indexű eleme).
A fejezet során azzal foglalkozunk, hogy milyen módon lehet megtalálni egy s∈X* sorozat k–adik elemét, illetve speciálisan a minimumát, maximumát és mediánját.
Algoritmusaink az s sorozat elemeit nem ismerik. Csak annyit tudnak tenni, hogy feltesznek si≤sj alakú kérdéseket, és pusztán ezek eredménye alapján adják meg, hogy melyik az l index, melyre sl a kívánt tulajdonságú elem. Gyakran az l index csak implicit módon van benne az algoritmus eredményében, a tényleges eredmény (sl) egy x változóban áll elő. A fejezet során csak ilyen, úgynevezett összehasonlításos algoritmusokkal foglalkozunk.
A szemléletesség kedvéért az összehasonlításban szereplő elemekre a kieséses sportversenyekhez hasonló terminológiát használunk. Ha valamely x≤y alakú kérdésre a válasz igen, akkor xi-t vesztesnek, míg yj-t győztesnek nevezzük. Ha még azt is tudjuk, hogy x≠y, akkor erős vesztesről, illetve erős győztesről beszélünk.
Legyen u és v két egyforma hosszú, X elemeiből képzett sorozat. Az u-t és v-t hasonlónak nevezzük, ha minden 1≤i,j≤|u| párra ui≤uj akkor és csak akkor, ha vi≤vj. Világos, hogy az összehasonlításos algoritmusok a hasonló sorozatokon egyformán működnek, emiatt ugyanazon kiválasztási eredményt is kell adniuk.
Mielőtt a megoldó algoritmusok elkészítésébe belefognánk, bizonyítunk két tételt arról, hogy legalább hány összehasonlítást kell tenni ahhoz, hogy egy sorozat maximumát, illetve a k–adik elemét megtaláljuk.
Tétel. Legyen MaxKiv egy minden bemenetre jól működő összehasonlításos maximumkereső eljárás. Ekkor ahhoz, hogy MaxKiv bármely n hosszúságú bemenetre a garantáltan megtalálja a legnagyobb elemet, mindig legalább (n–1) összehasonlítást kell végeznie.
Természetesen hasonló tétel igaz a minimum kiválasztására is.
Bizonyítás. Az állítást teljes n-re vonatkozó indukcióval látjuk be.
Az n=1 esetben nyilván nincs szükség összehasonlításra, hiszen a maximum megegyezik a sorozat egyetlen elemével.
Tegyük fel, hogy az állítás n-nél(n ≥ 2) rövidebb sorozatok esetében igaz, és legyen segy n hosszú sorozat. Vizsgáljuk először azt az esetet, amikor az összehasonlítások legalább egyikében volt erős vesztes. Legyen az első ilyen összehasonlítás si≤sj. Vesztesként sj nem lehet a maximum, de nyilván azok az elemek sem, melyek a korábbi összehasonlítások alapján vesztők voltak sj -vel szemben. Jelöljük az így kizárt elemek számát m-el (nyilván m < n). Világos, hogy ezen kizárt elemek mindegyikére van legalább egy olyan összehasonlítás, melyben ők vesztők voltak. MaxKiv tehát legalább m összehasonlítást használ csak arra, hogy ezt az m elemet kizárja. A többi összehasonlítás a maradék n – m elemből választja ki maximumot, amihez indukciós feltételünk alapján szükséges legalább n – m – 1 darab összehasonlítás. Az összes összehasonlítások száma tehát legalább m + n – m – 1 = n – 1.
Térjünk rá arra az esetre, amikor egyik összehasonlítás sem eredményez vesztest. Tegyük fel, hogy MaxKiv legfeljebb n – 2 összehasonlítással helyesen meghatározta a maximumot; legyen ez x = sl. . Az n – 2 összehasonlítás legfeljebb n – 2 vesztest eredményezhet. Ezek közül legalább az egyik különbözik sl -től, legyen sr az egyik ilyen. Tekintsük most azt a z sorozatot, ahol minden elem egyenlő, kivéve zr -t, mely határozottan nagyobb a többinél. Világos, hogy erre a módosított sorozatra az algoritmus pontosan ugyanazokat az összehasonlításos eredményeket adja, ezért most is az l-et indexűt kell megneveznie maximumként. Ez pedig nyilván nem helyes, hiszen a módosított sorozatban nem zl, hanem zr a maximum.
Tétel. Legyen Kiv egy minden bemenetre jól működő, összehasonlításos, k–adik elemet kiválasztó algoritmus. Ekkor MÖkiv (n) ≥ n – 1 + min (n – 1, n – k) .
Átfogalmazva, a tétel azt mondja ki, hogy van olyan n hosszúságú 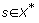 sorozat, melyre Kiv a k-adik elemet legalább n – 1 + min (n – 1, n – k) összehasonlítással tudja csak megtalálni.
sorozat, melyre Kiv a k-adik elemet legalább n – 1 + min (n – 1, n – k) összehasonlítással tudja csak megtalálni.
Bizonyítás. Csak a csupa különböző elemet tartalmazó sorozatok között keresünk ilyen n-et. Ha a Kiv eljárás egy s sorozatban helyesen megnevezi x = sl -et, mint az s sorozat k-adik elemét, akkor ez az elem a nála kisebb (k – 1) elemmel olyan k elemű halmazt alkot, melynek x a maximuma. Ehhez az előző tétel szerint szükséges közöttük legalább k – 1 összehasonlítás. Hasonló gondolattal láthatjuk be, hogy x és a nála nagyobb elemek között lennie kell n – k összehasonlításnak. Ez összesen n – 1 összehasonlítás.
Nevezzük nem lényeginek az olyan összehasonlításokat, melyeket a Kiv algoritmus a kis és nagy elemek között végezett. Ezek továbbiakat jelentenek az előbbi n – 1 összehasonlítás mellett. A kérdés az, hogy akármilyen kérdezési stratégia mellett van-e olyan n hosszú sorozat, mely esetében a kérdező nem lényegi kérdéseket is feltesz. Ha igen, akkor milyen kérdezési stratégia mellett lesz ezek száma a lehető legkisebb?
A kérdés megválaszolására az irodalomban ellenfél-módszernek nevezett technikát használják. Véleményünk szerint a furfangos válaszoló kifejezés jobban kifejezi a módszer lényegét, ezért a továbbiakban ezt elnevezést használjuk.
A technika és elnevezése a barkochba játékra vezethető vissza. Ennek lényegéhez tartozik az, hogy közösen rögzítenek egy véges halmazt, a keresési teret. Ezek után egyikük, a válaszoló kiválaszt ebből a halmazból egy elemet. A másik, a kérdező, igen-nem kérdésekkel megpróbálja ezt az elemet a lehető leghamarabb kitalálni. Egy kérdés az éppen aktuális keresési teret két részre bontja, és a válaszoló megmondja, a keresett elem melyik részben van. A kérdező ezt a részt tekintve aktuális keresési térnek ugyanígy halad tovább. Ha az aktuális keresési tér már csak egy elemű, akkor ezt az elemet adja válaszként.
A furfangos válaszoló a kérdezőt a lehető legtöbb kérdésre akarja kényszeríteni. Ebből a célból a játék elején nem rögzíti le előre a kitalálandó elemet, hanem a kérdező szempontjából lehető legkellemetlenebb módon folyamatosan változtatja. Ha valamely kérdés az aktuális keresési teret nem pontosan felezi, akkor furfangosan azt a választ adja, hogy a kitalált elem a nagyobbik részben van (persze ügyelnie kell válaszainak konzisztenciájára, különben a játék ellentmondásokhoz vezethet).
A 9.1. ábra a két kérdés utáni helyzetet mutatja, ahol a + jel a mindig a nagyobbik térfelet jelöli. A válaszoló a kitalálandó elemet előbb a + jelű, majd a (+,+)-os részbe helyezi át (ha eleve nem ott lett volna).
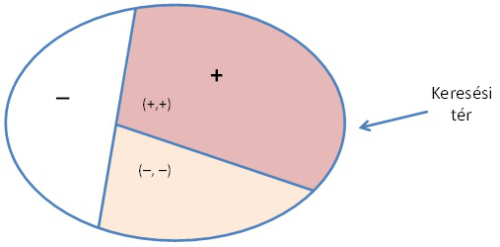 fej9_01_full.png9.1. ábra. A keresési tér
fej9_01_full.png9.1. ábra. A keresési térA furfangos válaszoló a kérdező stratégiájának legrosszabb esetét konstruálja meg. A kérdező a furfangos válaszoló ellen úgy védekezhet, hogy lehetőleg mindig olyan kérdést tesz fel, amely az aktuális keresési teret felezi. Ez a kérdezőnek a legrosszabb esetre nézve optimális (minimális kérdésszámmal járó) stratégiája.
Mi köze van mindennek az összehasonlításos algoritmusokhoz? Minden összehasonlításos algoritmust tekinthetünk kérdezőként, míg a kérdésekre adott válaszokat interpretálhatjuk úgy is, hogy azokat egy, a kérdezőtől független válaszoló adja meg. Az, hogy a válaszoló furfangos módon minél több kérdésre kényszeríti a kérdezőt, azt jelenti, hogy az adott algoritmus számára megkonstruál egy rossz esetet. Ha a kérdező (az algoritmus) – tudva mindezt – a lehető legjobb (optimális) kérdezési stratégiát használja, akkor ennek legrosszabb esete az összes, a feladatot megoldó algoritmus legrosszabb esetére vonatkozó alsó korlát lesz.
Térjünk vissza most az eredeti, k-adik elemet kiválasztó feladathoz. Lássuk először a furfangos válaszolónak a – bármely k-adik elemet kiválasztó algoritmusra működő – legrosszabb esetet konstruáló stratégiáját. Rögzít egy x∈X értéket, mely ebben a legrosszabb esetben a sorozat k-adik eleme lesz. Ezt az értéket majdan a kérdező által utoljára kérdezett elemnek adja. Egyébként az s sorozatot nem rögzíti előre, csak a kérdező kérdéseinek függvényében. A konzisztencia biztosítására készít magának egy táblázatot, melyben az adott indexű sorozatelem státuszát és pillanatnyi értékét tárolja.
A státuszok:
A furfangos válaszoló nem lényegi kérdésekre kényszerítő stratégiája – a később említendő megszorításokkal – a következő:
1.N,N típusú kérdés esetében az elsőt x-nél kisebbre, a másodikat x-nél nagyobbra rögzíti a megfelelő bejegyzéssel együtt, és megadja a rögzítésnek megfelelő választ.
2.L,N ,illetve S,N típusú kérdésnél az eddig nem kérdezett elemet a másik oldalra rögzíti, kiadva az ennek megfelelő választ.
3.S,L típusú kérdésnél a már rögzített értékeknek megfelelő választ ad.
4.Az utoljára rögzített elem értékét x-re, bejegyzését U-ra állítja.
A megszorítás az, hogy nem keletkezhet (k – 1)-nél több S bejegyzésű és (n – k) -nál több L bejegyzésű elem. Kicsit másképp fogalmazva, ha az egyik irány telítődött, akkor a bejegyzést és az értékét a másik oldalra kell állítani; az utolsót pedig U-ra.
Minden olyan hasonlítás, melyben van N bejegyzésű elem és még egyik irány sem telített, nem lényegi lesz. Ezek száma a kérdező stratégiájától függő. Ha nem szerencsésen kérdez, akkor akár (n – 2) is lehet az ilyen kérdések száma. (Az első kérdéstől eltekintve, mely mindkét irányt telíti, a többi kérdésnél 1-el telítődik valamelyik oldal). Ha viszont a kérdező ügyes és N,N bejegyzésű párokat kérdez, akkor minden kérdés telíti mindkét oldalt, ezért a kikényszerített nem lényegi kérdések száma optimális esetben min(k –1, n – k) lesz.
Azt kaptuk tehát, hogy legrosszabb esetben a nem lényegi kérdések száma még az optimális stratégiánál is min(k –1, n – k) . Ezzel a bizonyítást befejeztük.
Maximum, illetve minimum esetében ( k = n, illetve k = 1) a minimum egyik tagja 0, ezért visszakapjuk ez előző tétel állítását. A medián esetében, vagyis ha 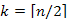 , pedig min ( k – 1, n – k) = min(
, pedig min ( k – 1, n – k) = min(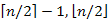 ), ami könnyen látható módon
), ami könnyen látható módon 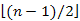 -vel egyenlő.
-vel egyenlő.
Összeadva ezt (n – 1) -gyel, az alsó korlátra 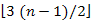 adódik. Például n = 5 esetében ez az alsó korlát
adódik. Például n = 5 esetében ez az alsó korlát 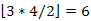 .
.
Foglalkozzunk először a maximum kiválasztással (a minimum kiválasztása ennek analogonja)!
Formálisan is felírjuk a maximum-kiválasztás feladatát, majd megadjuk a jól ismert és sokszor használt megoldó algoritmust.
Feladat: Valamely s∈X* sorozat maximumának megkeresése.
Deklaráció: 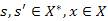
Előfeltétel: 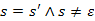
Utófeltétel: 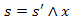 az s maximális eleme.
az s maximális eleme.
Egy megoldó algoritmus – legyen a neve MaxKiv – a következő:
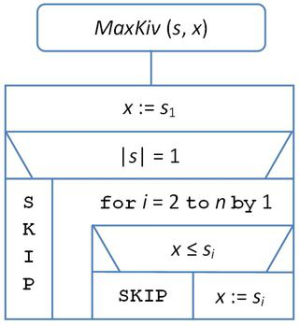 fej9_02_full.png9.2. ábra. Maximum kiválasztás algoritmusa
fej9_02_full.png9.2. ábra. Maximum kiválasztás algoritmusaElemzés. A ciklus |s| – 1 -szer fut le, minden iterációs lépés egy összehasonlítást tartalmaz.
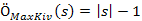 ,
,
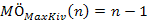 .
.
Ez a maximum-kiválasztó eljárás optimális, hiszen a maximum-tétel miatt ennél jobb nem készíthető.
Természetes gondolat, hogy a k-adik elemet annak definícióját követve úgy keressük meg, hogy s-et valamilyen rendezési módszerrel rendezzük, majd a rendezett sorozat k indexű tagját adjuk eredményül. Mivel egy n elemű sorozat rendezésénél az összehasonlítások száma legalább n log nagyságrendű, ez a megoldás távol van a kiválasztási tételben megadott lineáris alsó korláttól. Ennek magyarázata kézenfekvő. Ahhoz, hogy egy x elemről detektáljuk, hogy az s sorozat k-adik eleme, valójában elegendő volna találni a sorozatban (k – 1) nála kisebb-egyenlő és |s| – k nála a nagyobb-egyenlő elemet. A teljes rendezés felesleges többletmunkával jár, hiszen nem csak a kisebb-egyenlő és nagyobb-egyenlő elemeket adja meg, hanem azokat még – a feladat szempontjából feleslegesen – rendezi is. A következő algoritmus ezen a meggondoláson alapul.
Feladat: Valamely s∈X* sorozat k-adik elemének megkeresése.
Deklaráció: 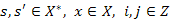
Előfeltétel: 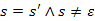
Utófeltétel: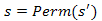 és x az
és x az 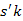 –adik eleme
–adik eleme
A k-adik elemet kiválasztó Kiv(s,k,x) algoritmus a Szetvag(s,i) eljárással s-et úgy rendezi át, hogy a sorozat eredetileg legutolsó elemét a helyére viszi olyan módon, hogy tőle balra csak nálánál kisebb-egyenlő elemek, míg tőle jobbra nagyobb elemek kerülnek. Ha ez az elem a i –edik helyre került, akkor k = i esetén készen vagyunk, x=si a keresett elem. Ha k < i, akkor az első felének, skicsi -nek a k –adik elemét kell tovább keresni, egyébként pedig a második felében, snagy-ban a (k – i)-ediket kell meghatározni, ugyanezzel a módszerrel.
Ennek megfelelően algoritmusunk rekurzív lesz. A Kiv(s,k,x) eljárás programja a következő:
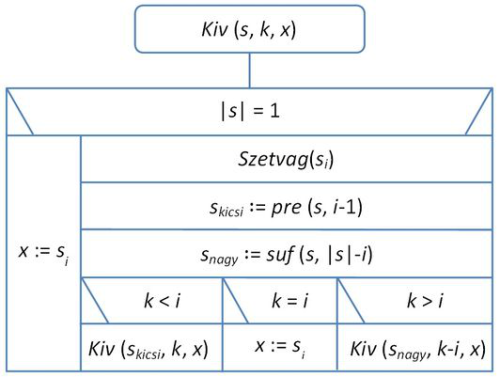 fej9_03_full.png9.3. ábra. A kiv(s,k,x) algoritmusa
fej9_03_full.png9.3. ábra. A kiv(s,k,x) algoritmusaElemzés. Most is az összehasonlítások számát számoljuk. A Szetvag(s,i) eljárás nyilván ( n – 1) összehasonlítással működik. A Kiv a legrosszabb esete az, ha a szétvágás mindig 1-gyel csökkenti azt a méretet, melyben a tovább kell keresnünk. Ilyenkor az összehasonlítások száma az első ( n – 1) egész szám összege.
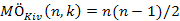
A legjobb eset az, amikor a sorozat utolsó eleme pontosan a k –adik ( k = i), hiszen ekkor azonnal leállhatunk:
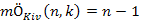
Mivel a legrosszabb és legrosszabb eset összehasonlításainak a száma nagyságrendben különböző, ezért érdekes megvizsgálni, hogy melyik az, amelyik inkább dominál. Az egyszerűség kedvéért tegyük fel, hogy s–et az 1, 2, ... , n permutációi alkotják, egyforma 1/n! valószínűséggel. Arra vagyunk kíváncsiak, hogy mit mondhatunk az 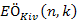 várható értékről.
várható értékről.
Tétel. Tetszőleges  esetén a Kiv(s,k,x) eljárás végrehajtott összehasonlításainak várható számára
esetén a Kiv(s,k,x) eljárás végrehajtott összehasonlításainak várható számára 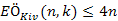 .
.
Bizonyítás. (n-re vonatkozó indukcióval) Kis n-ekre ( n= 0, 1) az állítás nyilvánvalóan igaz. Igazoljuk az állítást n ≥ 2-re, feltételezve, hogy kisebb elemszámra az állítás már igaz. Vezessük be a következő függvényeket:
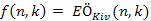
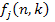
Amennyiben j = k, akkor 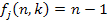 .
.
Ha j ≠ k, akkor a j-nél kisebb, illetve j-nél nagyobb elemek egymás közötti sorrendje is egyforma valószínűségű. Ezért k < j esetén az (n – 1)-hez hozzáadódik még f(j – 1, k), míg k > j esetén f(n – j, k – j).
Összefoglalva az alábbi összefüggést kapjuk a feltételes várható értékekre:
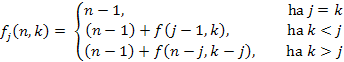
A teljes várható érték tétele alapján:
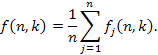
Beírva ide
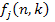
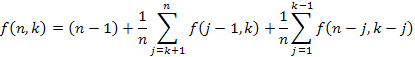
Mind j – 1, mind k – j kisebb n –nél, ezért ide beírhatjuk az indukciós feltétel szerinti becsléseket:
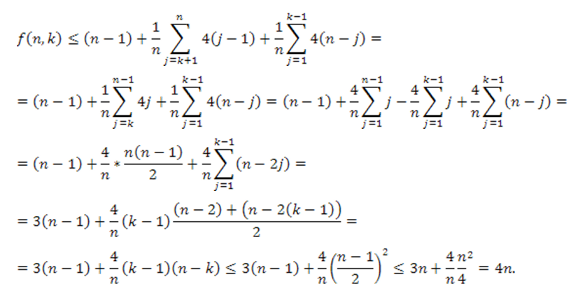
Közben alkalmaztuk a számtani sorozatok összegképletét, illetve a számtani és mértani közép közötti egyenlőtlenséget.
A Kiv(s,k,x) algoritmus összehasonlításainak várható számánál feltételeztük, hogy s-ben minden permutáció egyformán valószínű. A gyakorlatban ez sokszor nincs így, például a bemenő sorozat már közel rendezett is lehet. Ha ilyenkor valamilyen kis értékre keressük a k-adik elemet, akkor a méret csak lassan csökken. Ennek kivédésére véletlenített algoritmust alkalmazunk, nem az utolsó elemet, hanem a sorozat véletlenül választott tagját használja a szétvágás során.
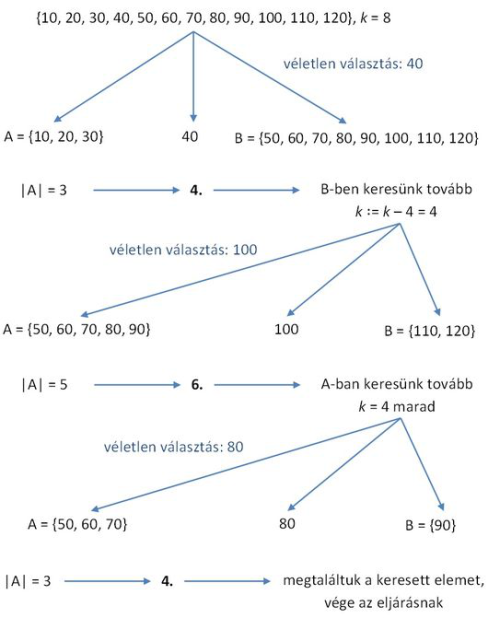 fej9_04_full.png9.4. ábra. A véletlenített algoritmus működése
fej9_04_full.png9.4. ábra. A véletlenített algoritmus működésePélda: Tekintsük a 10, 20,... 120 sorozatot, és keressük a k = 8-adik elemet!
1.A véletlen választás eredménye legyen 40, így ennek megfelelően bontsuk szét a sorozatot: A = 10, 20, 30 és B = 50, 60, ..., 120. Mivel |A| = 3, tudjuk, hogy a 40 a 4. elem a számsorozatban, ezért a 8-adik elemet az A sorozatban kell keresnünk. Mivel a számsorozat első 4 elemét leválasztottuk, ezért a B sorozatban már nem a 8-adik, hanem a 4. elemet keressük.
2.A bemenő sorozatunk 50, 60, ..., 120, a véletlen választás eredménye legyen 100, így A = 50, ..., 90 és B = 110, 120 sorozatok keletkeznek, így a 100 a 6. legkisebb elem, tovább kell tehát keresnünk a A halmazban, továbbra is a 4. elemet.
3.A bemenő sorozatunk 50, ..., 90, a véletlen választás eredménye legyen 80, így A = 50, ..., 90 és B = 90, tehát a 80 itt a 4. elem, vagyis megtaláltuk a k = 8-adik elemet.
Az algoritmus működését a 9.4. ábrával illusztráltuk.
Foglalkozzunk most azzal az esettel, amikor a sorozat típust az A[1..n] tömbben reprezentáljuk. Most az skicsi és snagysorozatok a tömb darabjai, ezért eljárásunk további lépéseiben már nem az egész tömbön működik, hanem általában egy u és v közötti darabján (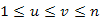 ). Emiatt az algoritmust kicsit általánosabban írjuk meg, a tömb A[u..v] szeletén. Olyan függvényeljárást készítünk, mely a k-adik elem értékét adja vissza.
). Emiatt az algoritmust kicsit általánosabban írjuk meg, a tömb A[u..v] szeletén. Olyan függvényeljárást készítünk, mely a k-adik elem értékét adja vissza.
Legyen VeletlenSzetvag olyan eljárás, mely a Szetvág eljárást az A[u..v] tömbdarabon egy onnan véletlenül választott elemmel végzi el úgy, hogy j-ben adja vissza a szétválasztó elem helyét. Világos, hogy ez az A[u..v]-nek az i=(j – u + 1)-edik eleme lesz. Ekkor i-t kell összehasonlítanunk k-val. Ha egyenlők, akkor készen vagyunk és ezt az értéket adjuk vissza. Ha i > k, akkor A[u..j – 1]-ben keressük tovább a k –adik elemet, míg i < k esetén A[j+1..v] -ben keressük a (k–i)-edik elemet.
A Kiv(A[u..v],k) rekurzív algoritmus külső hívása a teljes A[1..n]tömbbel és az eredetileg megadott k értékkel történik. Később az eljárás önmagát egy résztömbre hívja meg, esetleg módosított k értékkel. Az eljárás működésének leírását a 9.5. ábra tartalmazza.
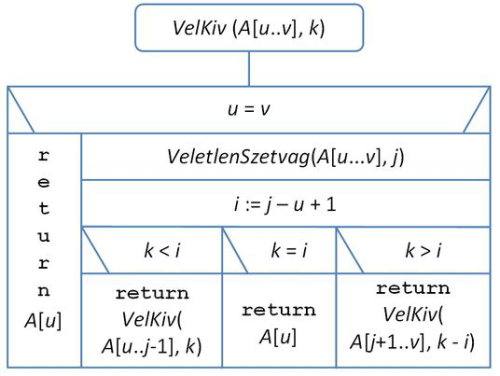 fej9_05_full.png9.5. ábra. A VelKiv algoritmus
fej9_05_full.png9.5. ábra. A VelKiv algoritmusElemzés. A véletlenített kiválasztás elemzése formálisan ugyanúgy történhet, mint a determinisztikus változaté. Az elvi eltérés abban van, hogy míg a Kiv eljárás esetében az input sorozat a véletlenszerű, addig a véletlenített változatban a véletlen magában az algoritmusban, nevezetesen a VeletlenSzetvag(A[u..v],j) eljárás működésében jelenik meg.
 |
 |
 |
A tananyag az ELTE - PPKE informatika tananyagfejlesztési projekt (TÁMOP-4.1.2.A/1-11/1-2011-0052) keretében valósult meg.
A tananyag elkészítéséhez az ELTESCORM keretrendszert használtuk.