A bináris keresőfa a kulcsos adatrekordok tárolásának egyik elsőként kialakult eszköze. Egyszerű tárolási elvet valósít meg: a legelső, a gyökérben elhelyezett rekord utáni kulcsokat a kisebb balra, nagyobb jobbra elv alapján illesztjük be a fába. A kiegyensúlyozással kiegészítve a tárolás hatékony adatszerkezetét kapjuk (AVL-fa, piros-fekete fa). A tárolási elvet pedig viszontlátjuk a ma leginkább használatos B-fáknál is.
Tekintsük adatrekordoknak azt a sorozatát, amelyben a kulcsok sorrendje a következő:
40, 110, 30, 60, 90, 10, 50, 20, 120, 80, 70, 100.
Ezekből az adatokból bináris fát építünk olyan módon, hogy az első elem, a 40-es alkotja a fa gyökerét, a további kulcsokat pedig az imént említett kisebb balra, nagyobb jobbra elv szerint szúrjuk be a keresőfába. A 110-es kulcs a gyökér jobb gyereke lesz, a 30-as pedig a bal gyereke. Ha már terjedelmesebb az épülő fa, akkor az aktuális kulcsnak a helyét a gyökértől indulva általában egy törött-vonal mentén keressük meg. Tekintsük a teljes fát bemutató 9.1. ábrán például a 80-as kulcsértéket, amellyel a gyökértől indulva jobbra-balra-jobbra-balra léptünk ahhoz, hogy el tudjuk helyezni a fában.
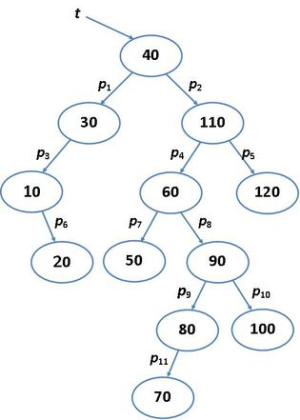 fej11_01_full.png9.1. ábra. Bináris keresőfa
fej11_01_full.png9.1. ábra. Bináris keresőfaAz ábrán látható bináris keresőfa az összes kulcsot tartalmazza. Jegyezzük meg, hogy a kulcsok más sorrendje is előállíthatja ugyanezt a fát. Ha például megcseréljük a 110-es és a 30-as kulcsok sorrendjét, nem lesz változás a kialakult keresőfában.
Az ábra az ADS szintű szemléletnek is megfelel, de a pointeres reprezentáció illusztrálására is alkalmas. A bináris keresőfát ugyanis általában láncolással valósítjuk meg. Az ábrán látható t,p1,...,p11 változók pointer értékűek, Ezek a bal és jobb gyerekcsúcsokra mutatnak, továbbá a fa minden adatelemében helyet kap a szülőre mutató pointer is, ahogyan a 9.2. ábrán látható (eredetileg a 7. fejezet, 7.2. ábrája). A szülő-pointereket az előző ábra nem tartalmazza, hogy a rajz könnyebben áttekinthető maradjon. (Eltekintünk az adatrekordoknak a kulcstól különböző mezőitől.)
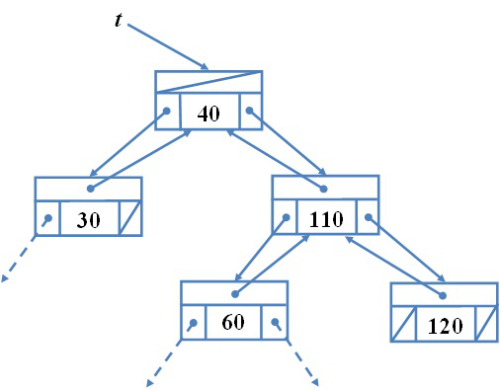 fej11_02_full.png9.2. ábra. Bináris keresőfa láncolt ábrázolása
fej11_02_full.png9.2. ábra. Bináris keresőfa láncolt ábrázolásaAdjuk meg a bináris keresőfa definícióját. A felépítés dinamikus szabálya után statikus meghatározást keresünk. A t bináris fát pontosan akkor mondjuk egyúttal bináris keresőfának, ha t bármely x csúcsára igaz az, hogy amennyiben y az x bal oldali részfájának egy csúcsa, illetve ha a z pont az x jobb oldali részfájának egy csúcsa, akkor
kulcs(y)<kulcs(x)<kulcs(z)
Az adatfeldolgozásban általában nem engedjük meg azonos kulcsok előfordulását. (Vegyük észre, hogy a definíció három univerzális kvantort tartalmaz. A meghatározás így arra az esetre is értelmes, ha az x csúcsnak nincsen bal vagy jobb oldali részfája.)
Figyeljünk fel arra, hogy nem lenne elég a fenti egyenlőtlenségeket csupán szülő-gyerek viszonylatban megkövetelni, hiszen akkor három szinten belül ellentmondásra juthatnánk a bináris keresőfa felépítésével. (Gondoljuk meg, hogy ha y és z csak gyerekcsúcsai lennének x-nek, akkor az ábrán a p11 által mutatott 70-es kulcsértéket például 55-re változtatva, a definíció teljesülne, holott az 55 nem kerülhet a 60-as csúcs jobb oldalára!)
A bináris keresőfa nevezetes tulajdonsága az, hogy inorder bejárással a kulcsokat rendezett sorozatként érjük el. Ez következik az inorder bejárás azon tulajdonságaiból, hogy
(1) a gyökeret középen, a bal oldali és a jobb oldali részfa bejárása között érintjük,
(2) a bal oldali részfa minden kulcsa kisebb, a jobb oldali minden kulcsa nagyobb, mint a gyökérben tárolt kulcs és
(3) mindkét oldali részfát inorder módon járjuk be.
Szemléletünk nem teszi szükségessé, hogy formálisan teljes indukciós bizonyítással lássuk be a bináris keresőfáknak ezt az alapvető tulajdonságát. (Az előbbi indoklás azonban már a bizonyításban alkalmazandó strukturális indukció lényegét tartalmazza.)
Ha rendezésre használnánk a bináris keresőfát, akkor abban az alkalmazásban nevezhetnénk rendezőfának. Mivel a rendezendő elemek között lehetnek egyenlők is, a fenti definícióban ≤ jeleket alkalmaznánk.)
A bináris keresőfára a keresés, a beszúrás és a törlés szokásos műveletei mellet bevezetjük a legkisebb kulcsérték megkeresését, valamint az adott kulcsértékre nagyság szerint rákövetkező kulcs megkeresésének műveletét is, hogy sorban végig tudjunk menni a kulcsok rendezett sorozatán, az elsőtől az utolsóig.
Az ismertetés során jellemző példákat adunk meg a keresőfa műveleteire, mindig a 9.1. ábrán látható adatszerkezetet véve alapul. Ezen az ábrán a keresőfa ADS szintű rajzát láthatjuk. A gyakorlatban a bináris fa láncolt megvalósítását használják, amelyet a 7.fejezetben ismertettünk. A műveletek algoritmusait is erre a pointeres reprezentációra adjuk meg, de a jelölésben élünk azzal a (tipográfiai) könnyítéssel, hogy a pointerre utaló → szimbólum helyett az ADS-szinten szokásos zárójeles írásmódot használjuk.
A műveleteknek egységes arculatot adunk. Mindegyik pointer típusú visszaadott értéket szolgáltat, ami adott esetben a hiba jelzésére is alkalmas (NIL pointer). Az eljárások paraméter-listáján mindig szerepel a bináris keresőfa t pointere. Ha szerepel további paraméter, akkor az egy eset kivételével szintén pointer típusú: vagy a fában mutat egy csúcsban elhelyezett rekordra, vagy a fán kívül összeállított adatrekordot címez. A kivételes eset a keresés művelete, amely egy kulcsértéket vár bemenő paraméterként.
A bináris keresőfa műveletei között alapvető egy adott k kulcsú rekord megkeresése. A keresés módja a keresőfa felépítésének elvén alapul. A gyökérnél kezdve összehasonlítjuk a keresett k értéket a csúcsban tárolt kulccsal. Ha az aktuális kulcs éppen megegyezik k-val, akkor megtaláltuk a keresett rekordot. Ha k kisebb, mint az aktuális kulcs, akkor balra lépve keresünk tovább, fordított esetben pedig a jobb oldalon folytatjuk a keresést. Ha olyan kulcsot keresünk, amely nem található a fában, akkor az eljárás egy levélcsúcsba található NIL pointeren áll meg. Az adott kulcsérték keresésének algoritmusát kivételesen két változatban is megadjuk, először a bináris fákhoz jól illeszkedő rekurzív eljárás formájában (lásd: 9.3. ábra).
Az eljárás hívása a következő értékadással történik:
r:=Keres(t,k)
ahol t a bináris keresőfa pointere és k a keresendő kulcs. Az eljárás az r pointer típusú változónak visszaadja a k kulcsú rekord címét, ha ilyet tartalmaz a keresőfa, illetve NIL-t ad vissza ellenkező esetben, ha a t nem tartalmazza a k kulcsot.
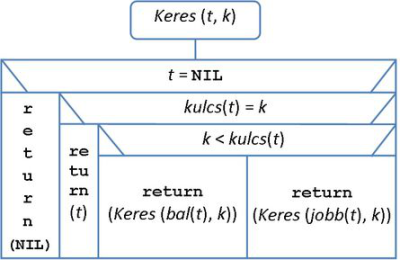 fej11_03_full.png9.3. ábra. A keresés műveletének rekurzív algoritmusa
fej11_03_full.png9.3. ábra. A keresés műveletének rekurzív algoritmusaPéldák a 9.1. ábrára való hivatkozással:
(1) 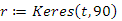
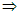
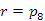
(2) 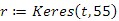
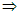
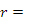 NIL
NIL
A keresés eljárásának iteratív változatát 9.4. ábra tartalmazza. A további műveletek esetén az iteratív változatot részesítjük előnyben.
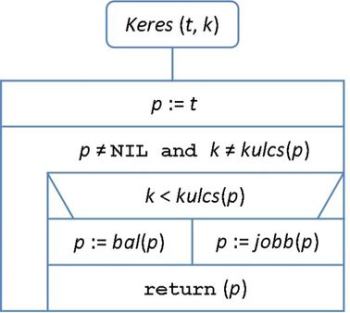 fej11_05_full.png9.4. ábra. A keresés műveletének iteratív algoritmusa
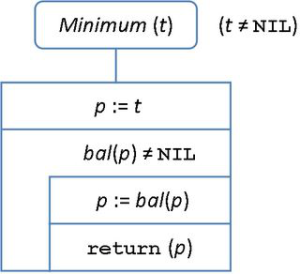
fej11_05_full.png9.4. ábra. A keresés műveletének iteratív algoritmusaEgy nem üres bináris keresőfában úgy jutunk el a minimális kulcsot tároló csúcshoz, hogy a gyökértől indulva mindig a bal oldali pointeren lépünk tovább. Ha már nem vezet tovább balra út, akkor megtaláltuk a legkisebb kulcsot.
Az eljárás hívása az
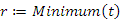
értékadással történik. Esetünkben az eljárás mindig balra lépve megtalálja a minimális 10-es kulcsértéket, és visszaadja annak pointerét az r változónak, azaz 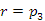 lesz. Az algoritmus a 9.5. ábrán adtuk meg.
lesz. Az algoritmus a 9.5. ábrán adtuk meg.
 fej11_06_full.png9.5. ábra. A minimális kulcs megkeresése
fej11_06_full.png9.5. ábra. A minimális kulcs megkereséseMegjegyezzük, hogy a minimális kulcsot tartalmazó csúcsnak lehet jobb oldali gyereke, de abban nagyobb kulcsérték található.
Egy adatokat tároló struktúrában, ha csak lehet, biztosítani kell azt, hogy a rekordokat kulcsaik növekvő sorrendjében érjük el. Ehhez szükséges az, hogy ki tudjuk választani a minimális kulcsú rekordot. Ezt a műveletet vezettük be az előző pontban. Most a rákövetkező kulcs megkeresésének műveletét adjuk meg.
Ha a bináris keresőfában a p pointer adott kulcsú rekordra mutat (és az nem a legnagyobb kulcsérték), akkor a következő kulcsérték megtalálásának két esetét kell észrevennünk. A most következő meggondolások alapján írtuk meg a 9.6. ábrán szereplő algoritmust.
Tekintsük először a 60-as kulcsérték rákövetkezőjének, a 70-es kulcsnak a megkeresését. Az megfelelő művelet meghívása és annak eredménye:
(1) 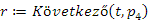
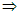
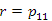
A következő kulcsot úgy találjuk meg, hogy a 60-as kulcsérték jobb oldali részfájában, ahol a közvetlen nagyobb kulcsokat találjuk, megkeressük a legkisebb kulcsot az előzőleg bevezetett Minimum művelettel.
Ha a 100-as kulcsérték rákövetkezőjét szeretnénk megkeresni, akkor a következő utasítást adjuk ki:
(2) 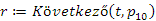
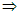
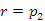
Most ezzel előző stratégiával nem élhetünk, mivel a kulcsnak nincs jobb oldali leágazása. Ekkor inverz szemlélettel azt a pontot keressük meg a fában, amelynek a szóban forgó 100-as kulcs a megelőzője. Annak a csúcsnak a 100-as kulcs a baloldali részfájában a maximális érték, amelyhez a részfában jobb pointerek sorozatán jut el. Ezt a keresési utat kell a 100-as csúcsból indulva megfordítani.
Általában, az adott pontból szülő pointereken megyünk addig, amíg azok – a szülőből nézve – jobb gyerekre mutató pointerek (ez a sorozat lehet üres is). Utána még egy lépést kell tennünk felfelé egy szülő pointeren, amely – ismét a szülő csúcshoz viszonyítva – bal gyerekhez vezet.
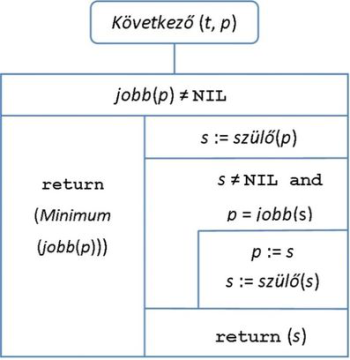 fej11_09_full.png9.6. ábra. A nagyság szerint következő kulcs megkeresése
fej11_09_full.png9.6. ábra. A nagyság szerint következő kulcs megkereséseA bináris fában található maximális kulcsnak nincs rákövetkezője. Ilyenkor a keresés, ezzel összhangban, NIL pointert ad vissza:
(3) 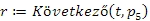
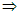
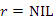
Ezt az esetet az előző, második programág kezeli azzal, hogy a nulla-hosszúságú balra fölfelé vezető út után nem képes egy lépést tenni jobbra fölfelé.
A bináris keresőfába úgy illeszthetünk be – csúcs formájában - egy új kulcsos rekordot, hogy összeállítjuk az új tartalmat egy pontosan olyan szerkezetű rekordban, mint amilyen többi rekord. Az új rekord rendelkezik azzal a három pointer mezővel, amellyel a fában mindegyik fel van szerelve; ezek a bal és a jobb gyerekre, valamint a szülőre mutatnak.
Az új rekordra mutató pointert adjuk oda a beszúrást végző eljárásnak, amely a már többször látott, balra-jobbra összehasonlító és lépegető stratégiával megkeresi az új kulcs helyét és létrehozza a bináris keresőfa egy új levelét.
Ha a beillesztendő kulcs különbözik a fa mindegyik kulcsától, akkor sikeres lesz az elhelyezés (ezt az jelzi, hogy az eljárás a p pointer étékét adja vissza), ha viszont megegyezik valamely kulcsértékkel a fában, akkor a sikertelen beszúrást a visszaadott NIL érték jelzi.
A beszúró algoritmus működése a 9.7. ábráról olvasható le.
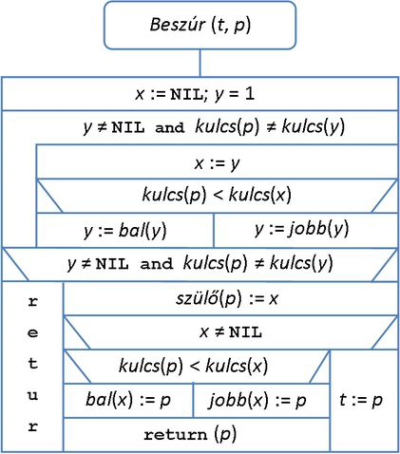 fej11_10_full.png9.7. ábra. Kulcsos rekord beszúrása bináris keresőfába
fej11_10_full.png9.7. ábra. Kulcsos rekord beszúrása bináris keresőfábaHa összeállítunk egy olyan új rekordot, amelynek a kulcsa a 45 érték és a p pointer mutat a rekordra, akkor a beszúrás hívása és eredménye a következő:
(1) 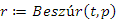
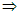
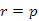
A keresőfába beillesztett új, 45-ös kulcsértékű csúcsot megtaláljuk a 9.9. ábrán.
Ha a bináris keresőfa adott kulcsú rekordját törölni szeretnénk, akkor rá kell állni egy pointerrel ahhoz, hogy a törlés műveletét meghívhassuk. A törlésnek három esetét különböztetjük meg, ahogyan ez a 9.8. ábrán elhelyezett algoritmus-leírásban követhető.
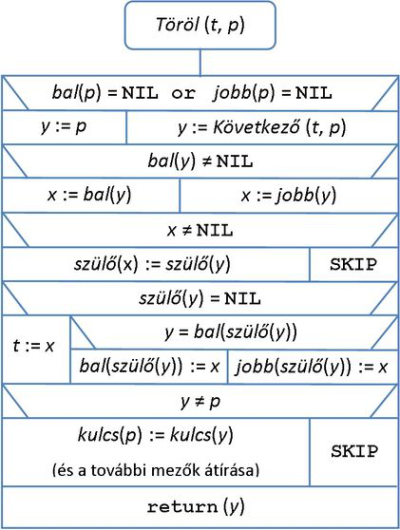 fej11_11_full.png9.8. ábra. Adott kulcsérték törlése bináris keresőfából
fej11_11_full.png9.8. ábra. Adott kulcsérték törlése bináris keresőfábólAz első esetben a törlendő elem egy levél, tehát nincs sem bal, sem jobb oldali leágazása. Töröljük például a p10 pointer által mutatott 100-as kulcsú elemet:
(1) 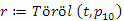
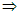
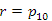
A törlés ebben az esetben a legegyszerűbb. A törlendő elemet és a szülőjét szétláncoljuk, és a fából így eltávolított csúcs pointerét a felhasználó rendelkezésére bocsátjuk. Esetünkben az eljárás a 100 kulcsértékű rekord szülőjének, a 90-es csúcsnak a jobb oldali pointerét NIL-re állítja, a p10-es mutató értékét pedig visszaadja a hívás helyére (lásd: 9.9. ábra).
A második eset olyan elem törléséről szól, amelynek egy gyereke van, azaz egyik oldalon egy részfa kapcsolódik hozzá, de a másik oldala üres. Töröljük például a p3 pointer által azonosított 10-es kulcsú elemet:
(2) 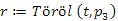
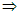
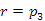
A törlés ebben az esetben sem nehéz. Ezúttal a törlendő elemet nem csak a szülőjétől, hanem gyerekétől is függetlenné tesszük, és a fából így eltávolított csúcs pointerét visszaadjuk a művelet hívásának a helyére. Ezután a törölt elemnek a szülő és gyerek csúcsát még össze kell kapcsolni, hogy ne maradjon szakadás a fában. Esetünkben az eljárás a 10-es kulcsértékű rekord szülőjének, a 30-as csúcsnak a bal oldali pointerét 20-as csúcsra állítja, ennek szülő pointerét pedig a 30-asra, a p3-as mutató értékét pedig visszaadja (lásd: 9.9. ábra).
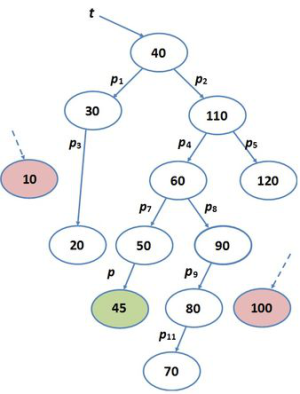 fej11_13_full.png9.9. ábra. A bináris keresőfa három művelet végrehajtása után
fej11_13_full.png9.9. ábra. A bináris keresőfa három művelet végrehajtása után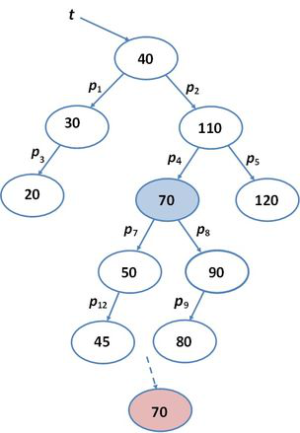 fej11_14_full.png9.10. ábra. A bináris keresőfa az újabb törlés végrehajtása után
fej11_14_full.png9.10. ábra. A bináris keresőfa az újabb törlés végrehajtása utánA törlés harmadik esete egy olyan csúcsra vonatkozik, amely mindkét oldali gyerekcsúccsal (részfával) rendelkezik. Olyan megoldást keresünk, amely nem növeli a keresőfa magasságát. A törlésre vonatkozó előírást logikainak fogjuk fel, és eltávolítjuk ugyan a megjelölt kulcsú rekordot, de ezt fizikailag egy másik elemet törlésével oldjuk meg.
Megkeressük a törlésre váró elem jobb oldali részfájában a minimális kulcsot és fizikailag azt a csúcsot töröljük, előbb azonban a benne tárolt értékkel felülírjuk a törlésre kijelölt csúcs tartalmát. Azért választjuk ezt a megoldást, mert a fizikailag törölt csúcsnak, mint egy részfa minimumának, nem lehet bal oldali gyereke, így az előzőleg tárgyalt első vagy második típusú törlés alkalmazható rá.
Töröljük például a p4 pointer által mutatott 60-as kulcsot a t keresőfából:
(3) 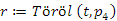
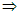
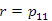 (!)
(!)
A 9.10. ábra szemléletesen mutatja be a törlés imént ismertetett módszerét. Láthatjuk azt is, hogy az eljárás által visszaadott mutató érték ebben a harmadik esetben nem a törlésre eredetileg kijelölt rekordra mutat, hanem annak a csúcsnak a pointere, amelyik fizikailag törlésre került.
A bináris keresőfa műveleteinek lépésszámát összefüggésbe hozzuk a fa magasságával. Meggondolásaink arra vezetnek, hogy famagasság nagyságrendben felülről korlátozza a műveletigényt. Eredményünk azt a célt vetíti elénk, hogy előnyös lenne a keresőfát minél inkább tömörített formában tartani, a műveletek hatékonysága miatt.
A bináris keresőfa várható magasságára próbálunk ezután becslést adni. Elméletileg érdekes kérdés, hogy nagyszámú, véletlen jellegű művelet elvégzése után milyen famagasságra számíthatunk. A válasz a gyakorlat számára is értelmezhető.
Ha sorra áttekintjük azt az öt műveletet, amelyet a bináris keresőfákra bevezettünk, akkor azt láthatjuk, hogy mindegyiknek a lényegi részét egy útvonal bejárása adja a fában. Ez az útvonal egy olyan útnak részét képezi, amely a fa gyökerétől valamely levélig terjed. Ennek a befoglaló útvonalnak a hossza attól függ, hogy milyen mélységben található az a levél, amelyben végződik. Minden esetre, a keresőfa magassága felső korlátját képezi a teljes útnak, így a szóban forgó művelet úthosszának is.
Ez minden egyes példánkon ellenőrizhető. Nézzük például a 90-es kulcsú rekord megkeresését, vagy a 60-as kulcsérték törlését. Ennek a két műveletnek a végrehajtása során bejárt két út ugyannak a 40 →70 gyökér-levél útvonalnak a részét képezi.
A műveletek lépésszáma lényegében megegyezik a fában bejárt útvonal hosszával, amelyhez még hozzá számítunk néhány (konstans számú) lépést. Azt mondhatjuk tehát, hogy bináris keresőfa mindegyik op műveletére érvényes az az állítás, hogy lépésszámát nagyságrendben a fa 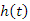 magassága felülről korlátozza:
magassága felülről korlátozza:
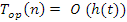
A bináris fa a magasságának az alsó korlátját a majdnem teljes fa összenyomott állapotában veszi fel, a magasság legnagyobb értékét pedig egy láncszerű fa esetén kapjuk. Érvényes a következő összefüggés:
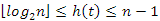
A két összefüggés alapján a bináris fa műveleteire a következőket állíthatjuk az általános (tetszőleges egyedi) esetben, valamint a legkedvezőbb, illetve a legkedvezőtlenebb esetben:
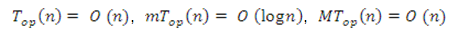
A meggondolások és az eredmények alapján kitűzhetjük azt a programot, amelynek a megoldását a következő fejezetek adják. A műveletek hatékonysága érdekében jó lenne a bináris keresőfa magasságát karbantartani; ha lehetséges, akkor 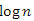 -es nagyságrendben korlátozni.
-es nagyságrendben korlátozni.
Az a természetes módon adódó kérdés, hogy nagyszámú véletlen jellegű művelet elvégzése után mennyi lesz a bináris keresőfa várható magassága, túl általános ahhoz, hogy meg tudjuk válaszolni.
A famagasság helyett egy hasonló és könnyen számolható speciális értéket vizsgálunk. A 9.1. ábrán látható t fa magassága 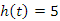 , míg átlagos csúcsmagassága 30/12=2,5. Érdemes külön megnevezni azt, hogy a számlálóban szereplő 30-as érték a t fa csúcsmagasság-összege (a 12 pedig a t fa pontjainak a száma, amit általában n-nel jelölünk.)
, míg átlagos csúcsmagassága 30/12=2,5. Érdemes külön megnevezni azt, hogy a számlálóban szereplő 30-as érték a t fa csúcsmagasság-összege (a 12 pedig a t fa pontjainak a száma, amit általában n-nel jelölünk.)
Ha nagyszámú bináris fára számolnánk átlagos csúcsmagasságot, akkor ez két átlagszámítást jelentene: egyet magukon a fákon, egyet pedig a fák teljes populációján. Áttekinthetőbb lesz a számítás, ha bevezetjük az n pontot tartalmazó bináris fák átlagos (vagy várható) csúcsmagasság-összegét, amit 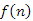 -nel jelölünk.
-nel jelölünk.
Az átlagos csúcsmagasság-összeget a következő módon értelmezhetjük: vegyük az 1,2,...,n kulcsok összes permutációját, mindből építsünk bináris keresőfát és számoljuk ki a csúcsok magasságösszegét is. Végül, képezzük az így meghatározott 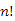 számú érték átlagát; erre vezettük be az
számú érték átlagát; erre vezettük be az 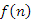 jelölést.
jelölést.
A valószínűségszámítás fogalmaival ez máshogyan is elmondható. Elméletben sorsoljuk ki véletlenszerűen egy permutáció1,2,...,n kulcsok összes permutációjából, ha mind egyformán valószínű. A magasságösszeg várható értékét ekkor egy elméleti kalkulussal számítjuk, és ugyanazt az értéket kapjuk, mintha az összes tényleges esetre átlagolnánk.
Végül, az 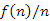 érték az egyes fákra értelmezhető átlagos csúcsmagasságok átlaga, illetve várható értéke, az összes
érték az egyes fákra értelmezhető átlagos csúcsmagasságok átlaga, illetve várható értéke, az összes 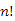 számú kulcssorozatot alapul véve.
számú kulcssorozatot alapul véve.
A nagyszámú véletlen művelet helyett egy speciális tevékenység-sorozatot tekintünk: adott n számú kulcsértékből felépítjük a keresőfát. Ennek során egymás után n-szer hajtjuk végre a fába történő beszúrás műveletét. A kulcsértékek – az általánosság megsértése nélkül – vehetők az az 1,2,...,n értékeknek.
Minden átlagszámítás mögött az adatoknak egy eloszlása húzódik meg, amelyet vagy ismernünk kell, vagy valamilyen feltevéssel kell élni arról, gyakorlati átlagot vagy elméleti várható értéket csak így tudunk számolni. Tételezzük fel, hogy az 1,2,...,n kulcsok minden sorrendje (permutációja) egyformán valószínű!
Ennyi előkészítés után megfogalmazzuk a feladatot. Számítsuk ki bináris keresőfa várható 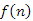 csúcsmagasság-összegét minden olyan tn fát alapul véve, amelyet az 1,2,...,n kulcsok sorozatából építünk fel. A véletlen sorozat elnevezés egyezményesen a permutáció egyenletes eloszlását jelenti. Ha meghatároztuk a várható csúcsmagasság-összeget, akkor azt n-nel osztva az egy fában mért csúcsmagasságok átlagának az
csúcsmagasság-összegét minden olyan tn fát alapul véve, amelyet az 1,2,...,n kulcsok sorozatából építünk fel. A véletlen sorozat elnevezés egyezményesen a permutáció egyenletes eloszlását jelenti. Ha meghatároztuk a várható csúcsmagasság-összeget, akkor azt n-nel osztva az egy fában mért csúcsmagasságok átlagának az 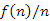 várható értékét kapjuk, ami már jellemzi a fa átlagos magasságát is:
várható értékét kapjuk, ami már jellemzi a fa átlagos magasságát is:
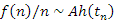
A bináris keresőfa felépítése során egy kulcs beépítése éppen annyi összehasonlítással jár, mint amilyen magasságban végül a megfelelő csúcs a fában elhelyezkedik. Például a k=90 kulcs beszúrása a t fába három összehasonlítást igényelt és valóban h(90)=3.
A keresett várható értéket nem egyszerre az összes kulcssorrendre számoljuk, hanem az összes permutációt n egyenlő számosságú részhalmazra bontjuk. Tekintsük az összes 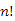 számú permutáció közül azokat, amelyekben a
számú permutáció közül azokat, amelyekben a 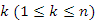 kulcsérték áll az első helyen. Azokat a fákat, amelyek az ilyen sorozatokból épülnek, általánosan illusztrálja a 9.11. ábra.
kulcsérték áll az első helyen. Azokat a fákat, amelyek az ilyen sorozatokból épülnek, általánosan illusztrálja a 9.11. ábra.
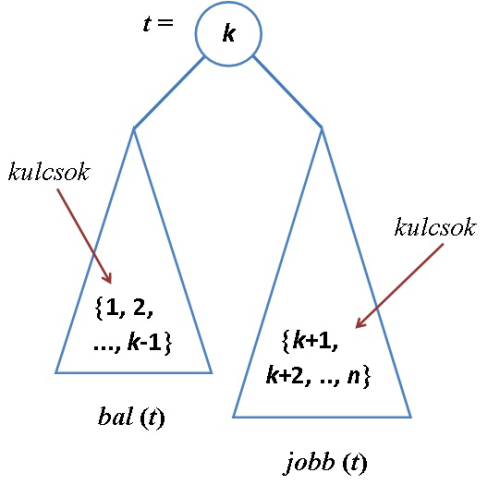 fej11_15_full.png9.11. ábra. Véletlen építésű bináris keresőfa átlagos létrehozási költsége
fej11_15_full.png9.11. ábra. Véletlen építésű bináris keresőfa átlagos létrehozási költségeHa minden ilyen 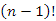 számú kulcssorozatra kiszámítjuk a csúcsmagasság-összeg várható értékét, akkor azok átlagaként kapjuk a keresett
számú kulcssorozatra kiszámítjuk a csúcsmagasság-összeg várható értékét, akkor azok átlagaként kapjuk a keresett 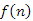 értéket. Jelölje f(n|k) a várható csúcsmagasság-összeget abban az esetben, ha a k kulcs érkezik első helyen és így azt a fa gyökerében helyezzük el. Ekkor
értéket. Jelölje f(n|k) a várható csúcsmagasság-összeget abban az esetben, ha a k kulcs érkezik első helyen és így azt a fa gyökerében helyezzük el. Ekkor
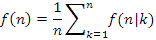
A 9.11. ábra alapján látható, hogy erre a fára az átlagos csúcsmagasság-összeg számításában figyelembe lehet venni azt, hogy a k-tól különböző csúcsok melyik oldali részfába kerültek (az 1, 2, ..., k-1 balra, a k+1, ..., n jobbra), miután egy összehasonlítás a gyökérrel ezt eldöntötte.
f(n|k) = (k - 1) + f(k - 1) + (n – k) + f(n – k)
Helyettesítsük ezt az összefüggést a fenti egyenlőségbe és végezzünk átalakításokat:
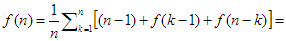
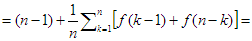
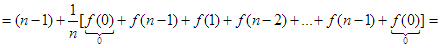
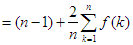
Végül, a nyilvánvaló f(1)=0 összefüggés figyelembe vételével a következő rekurzív egyenletet kapjuk:
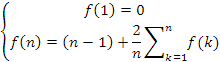
Azt állítjuk, hogy ennek a rekurzív egyenletnek a megoldására teljesül a következő felső becslés:
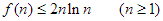
A bizonyítást teljes indukcióval végezzük.
Az 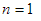 esetben egyetlen pontból álló bináris fáról van szó, amelyben a csúcs elhelyezése összehasonlítás nélkül történt, tehát valóban igaz, hogy
esetben egyetlen pontból álló bináris fáról van szó, amelyben a csúcs elhelyezése összehasonlítás nélkül történt, tehát valóban igaz, hogy 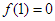 . A bizonyítandó becslés fennáll, mivel
. A bizonyítandó becslés fennáll, mivel 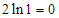 .
.
(Az 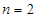 esetet már nem kellene ellenőrizni, ám ha engedünk a kíváncsiságunknak, akkor megnyugtató, hogy
esetet már nem kellene ellenőrizni, ám ha engedünk a kíváncsiságunknak, akkor megnyugtató, hogy 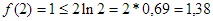 .)
.)
Tegyük fel, hogy igaz a bizonyítandó felső becslés 1, 2, ..., 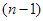 -re. Ekkor
-re. Ekkor
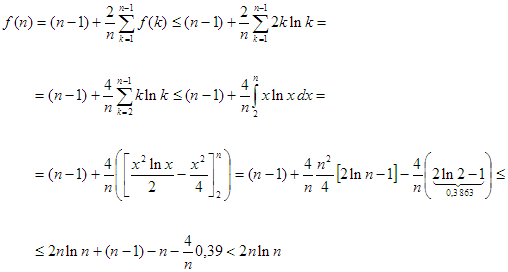
Azt kaptuk, hogy 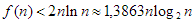 , ami átrendezve az
, ami átrendezve az
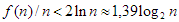
eredményre vezet. A bebizonyított becslést úgy értelmezhetjük, hogy a véletlen kulcssorozatból felépített bináris keresőfa várható csúcsmagasság-átlaga – kis konstans szorzóval – a 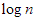 -es nagyságrendű marad.
-es nagyságrendű marad.
A tényleges famagasság átlaga szimulációval becsülhető. Ennek eredményeképpen hasonló állítás fogalmazható meg 2 körüli konstanssal.
Eredményünk nagyon megnyugtatónak tűnik, de csak abban az esetben garantált az, hogy a keresőfa várhatóan nem nyúlik meg, ha a kulcssorozat valóban véletlen, vagyis egyenletes eloszlásból származik. Ez a gyakorlati életben egyáltalán nem garantált. Gondoljunk arra, hogy mondjuk, egy cég életében az adatok (például napi kereskedelmi adatok) összegyűjtése adott rendet követ, így a véletlenszerűség biztosan torzul. Ezért a bináris keresőfa karbantartásának célkitűzését változatlanul érvényesnek tekintjük.
 |
 |
 |
A tananyag az ELTE - PPKE informatika tananyagfejlesztési projekt (TÁMOP-4.1.2.A/1-11/1-2011-0052) keretében valósult meg.
A tananyag elkészítéséhez az ELTESCORM keretrendszert használtuk.