Jegyzetünk 19. fejezetében tárgyaljuk azt a sokat által ismert tényt, hogy n tetszőleges elem összehasonlítás alapú rendezése leggyorsabban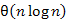 
összehasonlítással végezhető el. Bár nagy bemenetre jóval lassabbak, mégis hasznos megismerni az alábbi 
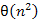összehasonlítást használó algoritmusokat. Nagy előnyük az egyszerűségük, ami nem csak a programozó számára jelent könnyebbséget, hanem abban is megnyilvánul, hogy rövid bemenetre gyorsabb futásidőt eredményeznek, mint az 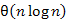-es társaik.
Például, n=8 elem esetén egy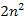 
lépésszámú algoritmus 
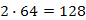időegység alatt fut le, míg egy 
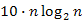futásidejű algoritmus 
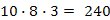időegység alatt.
Látni fogjuk, hogy sok esetben a legjobb konstans szorzó a beszúró rendezés esetén érhető el, míg a legkevesebb mozgatásra a maximumkiválasztó rendezésnek van szüksége. A buborékrendezést könnyű érthetősége és elterjedtsége miatt ismertetjük.
A buborékrendezés az egyik legrégebbi ismert rendezés. Lényege az, hogy a maximális elemet cserékkel felbuborékoltatjuk a tömb végére, és így visszavezetjük a problémát egy 1-el rövidebb rendezési feladatra.
A buborékoltatás úgy működik, hogy párosával (mintha egy két elem szélességű ablakot léptetnénk) haladunk végig az elemeken és a rossz sorrendben lévő párokat megcseréljük. Ezt az eljárást a 14.1. ábra szemlélteti.
fej14_01_full.png14.1. ábra. A buborékrendezés működéseBelátható, hogy így a legnagyobb elem eljut egészen a tömb végéig. (Ha több maximális elem is van a tömbben, akkor közülük a jobboldali jut el a tömb végére, mert egy egyenlő elempár esetén nem hajtunk végre cserét.) A második felbuborékoltatásnál már a tömb utolsó elemét nem kell figyelembe vennünk, hiszen tudjuk, hogy az jó helyen van.
Indukcióval látható, hogy a k-adik felbuborékoltatáskor az utolsó k-1 elem a tömb jobb szélén helyezkedik el, rendezve.
A rendezés algoritmusa a 14.2. ábrán látható. (A működés leírásában saját ciklusszervezést használtunk.)
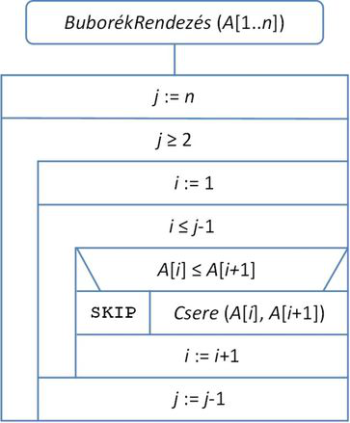fej14_02_full.png14.2. ábra. A buborékrendezés algoritmusaEbben a megfogalmazásban az indexek változtatásának a követése elvonhatja a figyelmet a lényegről, ezért tekintsük inkább a for ciklusos változatot, amely a 14.3. ábrán szerepel. A for ciklus, mint tudjuk, a by után megadott mértékben automatikusan növeli a ciklusváltozót minden iteráció végén.
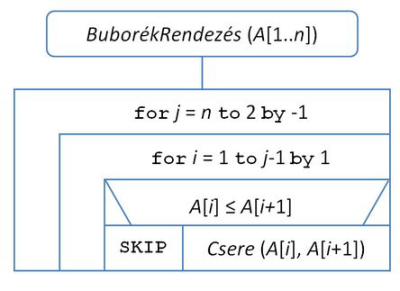fej14_03_full.png14.3. ábra. A buborékrendezés algoritmusa for ciklusokkalAz algoritmus egy külső és egy belső ciklusból áll. A külső ciklus j ciklusváltozója azt jelöli, hogy hányadik elemig rendezetlen még a tömb. Kezdetben természetesen mind az n elemet rendezetlennek vesszük, majd buborékoltatásonként eggyel rövidebb lesz a rendezetlen rész.
A belső ciklus i változója az aktuálisan vizsgált pár első elemének indexét jelöli. A ciklusmagban azt vizsgáljuk, hogy az i-edik és az i+1-edik elem jó sorrendben van-e, ezért az i változót csak j-1-ig növelhetjük.
A cserét most röviden jelöltük, valójában ez 3 mozgatást jelentene, egy külső változó felhasználásával. Könnyen észrevehetjük, hogy a buborékrendezés szükségtelenül sok mozgatást hajt végre, ezért nagyméretű adatoknál általában nem a legjobb választás.
A műveletigény részletes számítása megtalálható az 1. fejezetben. Az elemzést itt is megismételjük. A számolást az egyszerűség kedvéért külön-külön végezzük az összehasonlításokra és a cserékre.
Nézzük először az összehasonlítások Ö(n)-nel jelölt számát. A külső ciklus magja (n–1)-szer hajtódik végre, a belső ciklus ennek megfelelően rendre n–1, n–2, ..., 1 iterációt eredményez. Mivel a két szomszédos elem összehasonlítása a belső ciklusnak olyan utasítása, amely mindig végrehajtódik, ezért
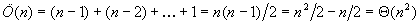
Az összehasonlítások száma ennek megfelelően négyzetes nagyságrendű.
Vizsgáljuk meg most a cserék Cs(n)-nel jelölt számát. Ez a szám már nem állandó, hanem a bemenő adatok függvénye. Nevezetesen, a cserék száma megegyezik az A[1..n] tömb elemei között fennálló inverziók számával:
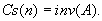
Valóban, minden csere pontosan egy inverziót szüntet meg a két szomszédos elem között, újat viszont nem hoz létre. A rendezett tömbben pedig nincs inverzió. Ha a tömb eleve rendezett, akkor egyetlen cserét sem kell végrehajtani.
A legtöbb cserét akkor kell végrehajtani, ha minden szomszédos elempár inverzióban áll, azaz akkor, ha a tömb éppen fordítva, nagyság szerint csökkenő módon rendezett. Ekkor a cserék maximális száma:
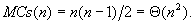
A cserék átlagos számának meghatározásához először is feltesszük, hogy a rendezendő számok minden permutációja egyenlő valószínűséggel fordul elő. (Az átlagos műveletigény számításához mindig ismerni kell a bemenő adatok valószínűségi eloszlását, vagy legalább is feltételezéssel kell élni arra nézve!) Az általánosság megszorítása nélkül vehetjük úgy, hogy az 1, 2, ..., n számokat kell rendeznünk, ha elfogadjuk azt a szokásos egyszerűsítést, hogy a rendezendő értékek mind különbözők.
A cserék számának átlagát nyilvánvalóan úgy kapjuk, hogy az 1, 2, ..., n elemek minden permutációjának inverziószámát összeadjuk és osztjuk a permutációk számával:
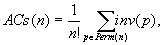
ahol Perm(n) az n elem összes permutációinak halmazát jelöli. Az összeg meghatározásánál nehézségbe ütközünk, ha megpróbáljuk azt megmondani, hogy adott n-re hány olyan permutáció van, amelyben i számú inverzió található (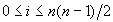
). Ehelyett célszerű párosítani a permutációkat úgy, hogy mindegyikkel párba állítjuk az inverzét, például a p=1423 és a pR=3241 alkot egy ilyen párt. Egy ilyen párban az inverziók száma együtt éppen a lehetséges 
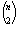-t teszi ki, például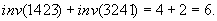 
Az állítás igazolására gondoljuk meg, hogy egy permutációban két elem pontosan akkor áll inverzióban, hogy ha az inverz permutációban nincs közöttük inverzió. A mondott párosításnak megfelelően minden két permutáció inverzióinak száma együttesen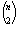, így az átlagos csereszám:
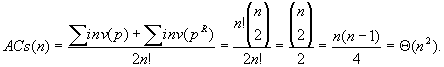
A cserék számának átlaga tehát a legnagyobb érték fele, de nagyságrendben ez így is n2-es.
A beszúró rendezés sok esetben a leggyorsabb négyzetes rendezés. Működése hasonló ahhoz, mint amikor lapjainkat rendezzük egy kártyajáték során. A rendezés fő lépése az, hogy az asztalon lévő rendezetlen saját pakliból elvesszük a felső lapot és beszúrjuk a kezünkben tartott rendezett lapok közé. Kezdetben a rendezett rész az első felvett lapból áll, majd n-1 beszúrás után lapjainkat már rendezett módon tartjuk a kezünkben.
A beszúró rendezés még nem említett előnye az, hogy nem csak tömbben tárolt elemek rendezésére alkalmas, hanem a láncolt listákra is könnyen alkalmazható.
A tömbben tárolt adatok rendezésére alkalmazott beszúró rendezés működését, egy-egy jellemző lépés megjelenítésével a 14.4. ábra szemlélteti.
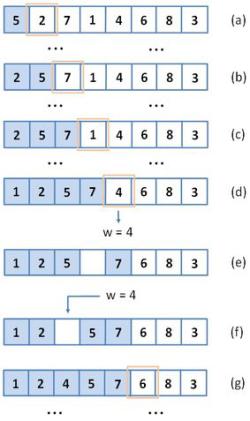fej14_12_full.png14.4. ábra. A beszúró rendezés működése tömbös megvalósítás eseténTömbös megvalósítás esetén a rendezett részt a tömb elején tároljuk, a rendezetlent pedig utána. Kezdetben csak a tömb első eleme rendezett. Minden iterációban a következőnek beszúrandó elemet elmentjük egy w változóba, majd az eddig rendezett rész nála nagyobb elemeit jobbra csúsztatjuk egy pozícióval.
A megfelelő számú léptetés után felszabadul a félretett beszúrandó elem számára a megfelelő hely. Ezután a beszúrandó elemet w-ből bemásoljuk a megfelelő helyre. A teljes algoritmus a 14.5. ábrán látható.
fej14_13_full.png14.5. ábra. A beszúró rendezés algoritmusa tömbös megvalósítás eseténAlgoritmusunk egy külső és egy belső ciklusból áll. A külső ciklus beszúrásonként lép egyet, míg a belső ciklus a beszúrás közbeni jobbra másolásokért felelős. A külső ciklus addig halad, amíg minden elemet be nem illesztettünk a helyére, a belső pedig addig, amíg meg nem találtuk az aktuálisan beszúrandó elem helyét.
A külső ciklus mindig n-1 alkalommal fut le, hiszen ennyi elemet kell beszúrnunk a rendezett részbe, ahhoz hogy az egész tömb rendezve legyen.
A belső ciklus műveletigénye változó. Legjobb esetben egyetlen összehasonlítást végez. Ez akkor fordul elő, ha a beszúrandó elem nagyobb vagy egyenlő az összes eddig rendezettnél. Legrosszabb esetben annyiszor hasonlítunk össze, ahány rendezett elem van és ugyanennyi másolást is végrehajtunk. Ez akkor történik, ha a beszúrandó elem kisebb az összes addig rendezettnél.
Összefoglalva, a műveletigény a következőképpen alakul:
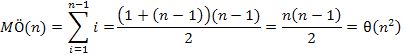
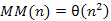
A legjobb eset az, ha a tömb eleve rendezet, ekkor elérhető az alábbi minimum:
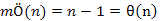
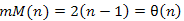
Átlagos műveletigényt itt nem számolunk.
Mivel minden beszúrás annyi inverziót szűntet meg, ahány elemet jobbra toltunk, és nem hoz létre új inverziót, ezért könnyen látható, hogy:
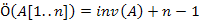
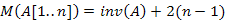
Alkalmas megvalósítással elérhető:
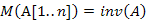
Ez az utolsó tulajdonság különösen gyorssá teszi a beszúró rendezést abban az esetben, ha a tömb eleve nagyjából rendezett volt.
Az algoritmus minden esetben gyorsabb a buborékrendezésnél. Azért is, mert egy elemet cserékkel helyretenni körülbelül 3-szor annyi másolást jelent, mint ha jobbra másolásokkal tennénk ezt.
A következő megjegyzés azért lényeges, mert kijelöli ennek a rendezésnek a helyét a többi között. Bár a beszúró rendezés cn2 idejű, rendkívül alacsony konstansa miatt szívesen használják, az oszd meg és uralkodj elvű,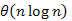 
futásidejű algoritmusok gyorsítására. Amikor kellően kicsi (log n méretű) részproblémákra osztják a feladatot, akkor már nem darabolják tovább, hanem a részeket beszúró rendezéssel rendezik. A nagyobb részproblémák megoldása az eredeti módon történik. Belátható, hogy így a rendezés 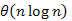futásidejű marad, hiszen legfeljebb 
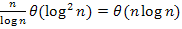pluszlépést hajtunk végre emiatt. Valójában azonban a kis konstans miatt így még sokat gyorsul is az algoritmus.
A beszúró rendezés további jó tulajdonsága, hogy láncolt listára is viszonylag könnyen megvalósítható. A 14.6. ábra a rendezés három fázisát (kezdő, egy közbülső és befejező állapotát) illusztrálja.
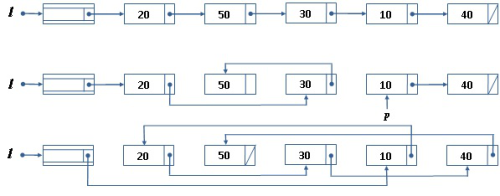fej14_14_full.png14.6. ábra. A beszúró rendezés működése fejelemes láncolt lista eseténAz algoritmus működése során a lista mindig két részt tartalmaz: az első fele már rendezett, míg a második felében még az eredeti sorrendben következnek az elemek. Úgy célszerű inicializálni ezt a helyzetet, hogy a rendezett rész kezdetben legyen az üres lista. Az eljárás végére viszont a rendezetlen rész fogy el. Egy közbülső állapot mutat az ábra második, középső listája.
Az algoritmus egy lépésében a második részből kiláncoljuk az első elemet és a rendezett részben befűzzük a helyére. Az algoritmus leírását a 14.7. és 14.8. ábrákon láthatjuk.
fej14_15_full.png14.7. ábra. A beszúró rendezés algoritmusa fejelemes láncolt lista eseténA listát kezdetben – a fentiek szerint – úgy vágjuk ketté, hogy l egy üres fejelemes listára, míg p az eredeti elemek fejelem nélküli listájára mutat. Az algoritmus során végig p mutat a rendezetlen elemek listájára, míg l a már rendezett elemek fejelemes listáját azonosítja. Az algoritmus második része egy ciklus, amely p-t lépteti és a q által mutatott kiláncolt elemre meghívja a beillesztés eljárását.
fej14_16_full.png14.8. ábra. A rendezettséget megtartó beillesztés algoritmusa fejelemes láncolt listáraA beillesztés algoritmusa úgy működik, hogy egy r mutatóval annyit lép l elemein, hogy az utolsó olyan elemre mutasson, amelyben még kisebb érték található, mint a beszúrandó elemben, amelyre a q pointer mutat. Ez után a q által mutatott listaelemet befűzi az r pointerű elem után.
A két megvalósítás között fennáll egy olyan különbség, a láncolt esetben a beszúrást balról jobbra hajtjuk végre, nem jobbról balra, mint a tömbös rendezésnél.
A láncolt megvalósítás futásideje közel azonos a tömbös megvalósítás futásidejével, ezért az elemzést nem részletezzük.
A maximum kiválasztó rendezés alapötlete – hasonlóan a buborékrendezéshez – az, hogy a legnagyobb elemnek a tömb végén van a helye, a rendezés szerint. Ezért kiválasztjuk a tömb maximális elemét, majd kicseréljük az utolsó elemével. Ezután már eggyel rövidebb tömbre alkalmazhatjuk a maximum kiválasztást és cserét. Ezt addig ismételjük, míg az egész tömb rendezetté válik. A 14.9. ábrán az eljárás működésnek néhány fázisa látható.
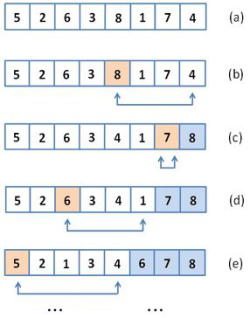fej14_17_full.png14.9. ábra. A maximum kiválasztó rendezés működéseAz algoritmus, amely leírásában hivatkozik a sokszor használt maximum kiválasztásra, a 14.10. ábrán látható.
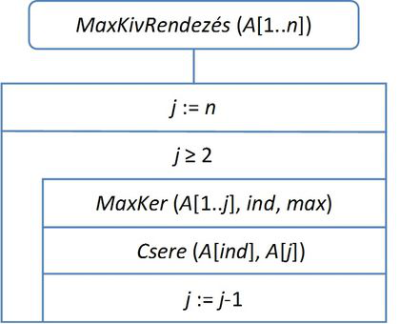fej14_18_full.png14.10. ábra. A maximum kiválasztó rendezés algoritmusaAz algoritmusban j-vel jelöljük a tömb rendezetlen részének hosszát. Ez kezdetben n, hiszen még az egész tömb rendezetlen. A ciklus minden lépésében kiválasztjuk a rendezetlen résztömb maximumát és kicseréljük az utolsó elemével. Így a rendezetlen rész j hosszát 1-el csökkentettük. Ha a rendezetlen rész hossza 2, akkor az utolsó iterációra kerülhet sor, hiszen egyetlen elem önmagában rendezettnek számít.
Érdekes eset az, amelyet a (c) ábrarész mutat: a maximális elem és a rendezetlen rész jobb szélső eleme ugyanaz, ilyenkor az elemet önmagával cseréljük meg.
Az algoritmus futásideje a következőképp áll elő: Az összehasonlítások száma az n-1 maximumkeresés összehasonlítás-számainak összege.
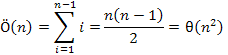
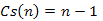
Ezek fix értékek minden lehetséges bemenetre. Ez a maximumkiválasztó rendezés egyik hátránya a beszúróval szemben, hogy nem tudja kihasználni a bemenet tulajdonságait, ahhoz, hogy kicsit gyorsabban fusson. Nagy előnye viszont, hogy 3(n – 1) mozgatást végez, nem pedig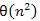 
-et. Ez akkor igazán előnyös, ha az elemek nagy mérete miatt a mozgatás lassabb művelet, mint az összehasonlítás.
 |
 |
 |
A tananyag az ELTE - PPKE informatika tananyagfejlesztési projekt (TÁMOP-4.1.2.A/1-11/1-2011-0052) keretében valósult meg.
A tananyag elkészítéséhez az ELTESCORM keretrendszert használtuk.