28. Mélységi bejárás

A gráfok két alapvető bejárási módja közül a mélységi bejárás ismertetése következik. A másik stratégiát, a szélességi bejárást a 23. fejezetben láttuk. Ott idéztük a Rónyai-Ivanyos-Szabó szerzőhármas Algoritmusok című könyvében olvasható szemléletes leírást a bejárási stratégiákról, illetve csak az egyikről: arról, amelyik a szélességi bejárást illusztrálja. Most idézzük a könyvből azt a módszert, amely „mélységében” igyekszik a városka lámpáit elérni.

Az irodalmi párhuzam után természetesen szabatosan megfogalmazzuk gráfokra is a feladatot, megadjuk és elemezzük annak megoldó algoritmusát.

28.1. A mélységi bejárás stratégiája

„Az öreg városka girbe-gurba utcáin bolyongó kopott emlékezetű lámpagyújtogató” másik eljárása a köztéri lámpák meggyújtására a mélységi bejárás elvét követei. Megint csak szabadon és tömören idézve a könyv szövegét, a lámpagyújtogató az első, majd a további lámpák felgyújtása után mindig egy olyan utcán indul tovább, amelyikben még nem lát fényt, és elérve a következő sarokhoz, meggyújtja az ott elhelyezett lámpát. Ha egy lámpa alól körülnézve már minden onnan kiinduló utcából fényt lát, akkor visszamegy arra, ahonnan ide érkezett, és onnan egy még meg nem gyújtott lámpa irányába indul. Ha ilyet nem lát, akkor innen is visszamegy a megelőző sarokra. Egy idő után visszaért eredeti kiinduló helyére, és ekkor már minden innen elérhető köztéri lámpa világít.

A leírásból – a stratégia mellett – kiemelünk három további jellemzőt. Míg az másik lámpagyújtogatási módszer végrehajtásában segítségére volta barátai, addig ezt az eljárást egyedül végezhette. A „kopott emlékezetének” itt valóban szerep jut, hiszen csak annyit kell megjegyeznie, hogy egy lámpához melyik utcán érkezett. A szöveg utal arra is, hogy a tevékenységét bárhol elkezdheti, nincs olyan meghatározott kiinduló pont, mint a barátokkal együttműködve a főtér volt.

Ha fentről néznénk a várost, ahogy kigyulladnak a lámpák, ezúttal azt látnánk, hogy egy pontból egy útvonal mentén terjed a világosság. Azután ez egy egyenletes ütemű terjedés megáll, és a visszasétálás idejét kivárva, világító lámpák útvonalának egy pontjából újra elindul a lámpagyújtási tevékenység egy útvonalon.

Ez mélységi bejárásnak a szemléletes alapelve, amelyet a fejezet végén elhelyezett 28.11. ábra illusztrál egy (csaknem kisvárosi kiterjedésű) gráfon, néhány pillanatfelvétel formájában.

Vissza a tartalomjegyzékhez

28.2. A mélységi bejárás szemléltetése

A mélységi bejárás kidolgozása felé lépve, megkülönböztetjük a csúcsok státuszát. Erre több, szemléletében különböző módszerrel találkozhatunk, amelyek végső ugyanazt a célt érik el. Itt a színezés eszközével élünk és három színt használunk. Attól függően színezzük a csúcsokat, hogy az illető csúcsot illetően a bejárás milyen fázisban van.

• Egy csúcs legyen fehér, ha még nem jutottunk el hozzá a bejárás során (kezdetben minden csúcs fehér).
• Egy csúcs legyen szürke, ha a bejárás során már elértük a csúcsot, de még nem állíthatjuk, hogy az illető csúcsból elérhető összes csúcsot meglátogattuk.
• A csúcs legyen fekete, ha azt mondhatjuk, hogy az illető csúcsból elérhető összes csúcsot már meglátogattuk és visszamehetünk (vagy már visszamentünk) az idevezető út megelőző csúcsára

A bejárás során tároljuk el, hogy egy csúcsot hányadikként értünk el, azaz hányadikként lett szürke és tároljuk el azt is, hogy hányadikként fejeztük be a csúcs, és a belőle elérhető csúcsok bejárását, azaz a csúcs hányadikként lett fekete. Az említett számokat nevezzük mélységi, illetve befejezési számnak, amelyeket az ábrákon a csúcsok címkéi alatt jelenítünk meg. (Alternatív szóhasználat: belépési, illetve kilépési számok.) Utalunk arra, hogy ezeknek a számoknak lényeges szerep jut majd az élek osztályozásánál.

A 28.1-4. ábrákon egy gráf mélységi bejárását követhetjük végig. (Az ábrasort egyben, szöveges megszakítás nélkül találjuk meg alább.) A példában szereplő gráfon a csúcsokból kimenő élek feldolgozási sorrendje legyen a rákövetkező csúcsok címkéje szerint növekedően, vagyis alfabetikusan rendezett (például a láncolt ábrázolásnál az éllista a csúcsok címkéje szerint rendezett).

Nézzük a 28.1. ábrát, amelyben a kezdőcsúcs legyen az 1-es csúcs. Legyen kezdetben minden csúcs fehér, és a mélységi és befejezési számuk is legyen az extremális 0. A kezdőcsúcsot érjük el elsőként, tehát színezzük szürkére, és a mélységi számát állítsuk be 1-re.

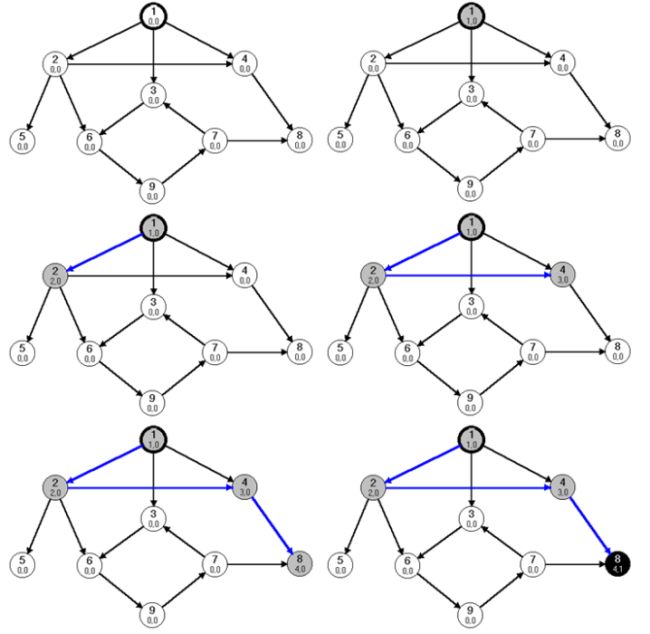A kép (nagyobb változata) külön ablakban is megtekinthető.fej28_s1_full.png28.1. ábra. A mélységi bejárás végrehajtása az első visszalépésig

A kép (nagyobb változata) külön ablakban is megtekinthető.fej28_s2_full.png28.2.ábra. A további csúcsok feltérképezése a bejárás során

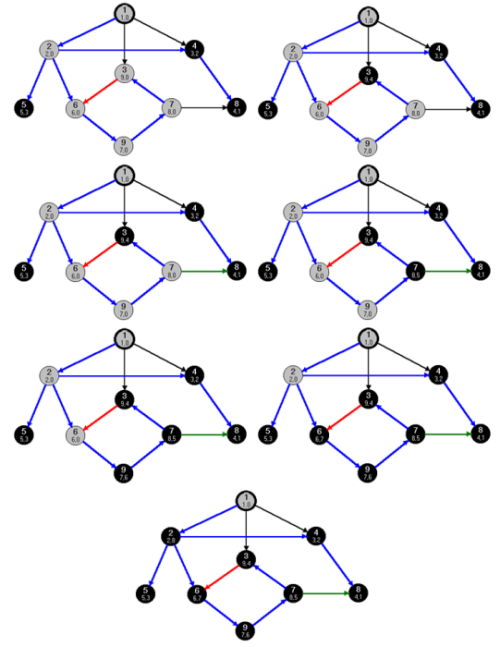A kép (nagyobb változata) külön ablakban is megtekinthető.fej28_s3_full.png28.3.ábra. A visszalépések végrehajtása a kiinduló csúcsig

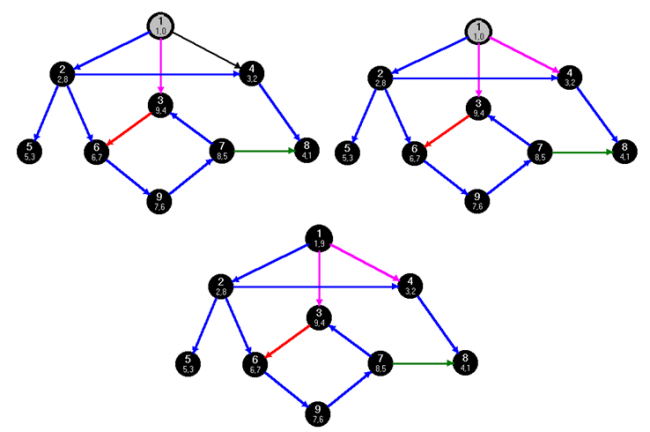A kép (nagyobb változata) külön ablakban is megtekinthető.fej28_s4_full.png28.4.ábra. A mélységi bejárás végső lépései

Az 1-es csúcsból három él vezet ki, de a kikötöttük, hogy az élek feldolgozási sorrendje legyen a szomszéd csúcsok címkéje szerint növekedően rendezett. Ekkor a 2-es csúcsot érjük el másodikként. Ezután harmadikként a 4-es csúcs, majd negyedikként a 8-as csúcs következik. Mivel a 8-as csúcsnak egyáltalán nincs szomszédja, bejárását befejeztük és a csúcsot feketére színezzük. Mivel a bejárás során a 8-as csúcs lett elsőként fekete, a befejezési száma 1-es lesz.

A bejárás során eddig megtett utunk 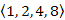. Most menjünk vissza az utolsó előtti 4-es csúcsra (lásd: 28.2. ábra). Mivel a 4-es csúcsnak sincs meg nem látogatott szomszédja, így ennek csúcs bejárását is befejeztük; színezzük a csúcsot feketére, és a bejárási számát állítsuk 2-re. Menjünk vissza a 2-es csúcshoz. A 2-es csúcsnak két olyan szomszédja is van, amelyet még nem látogattunk meg. Lépjünk a kisebb címkéjű csúcsba. Az 5-ös csúcs bejárását harmadikként fejezzük be. A 2-es csúcsból a bejárást a 6-os csúcs irányába folytatjuk. Tovább haladva, hetedikként elérjük a 9-es csúcsot (lásd: 28.2. ábra). Nyolcadikként következik a 7-es csúcs. Mivel a 3-as csúcs még fehér, azt érjük el kilencedikként

A 3-as csúcsból a 6-os csúcsba vezet él, azonban a 6-os csúcsot már bejártuk, a színe már nem fehér, erre már nem folytatjuk a bejárást. Mivel a 3-as csúcsból már nem vezet él fehér csúcsba, így a 3-as csúcs bejárását is befejeztük (lásd: 28.3. ábra). Visszamegyünk a 7-es csúcsba, ahol a sorrendben következő él, a 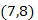mentén látjuk, hogy a 8-as csúcs színe már fekete. Mivel a 7-es csúcsnak nincs fehér szomszédja, így ötödikként befejeztük a bejárását. A 9-es csúcsnak a bejárását is befejeztük. Az úton ismét egy csúccsal visszamegyünk és befejezzük a 6-os csúcsot is. A 2-es csúcsra lépve, látható, hogy minden kimenő éle mentén már próbálkoztunk, így nyolcadikként azt is elhagyjuk.

Az 1-es csúcsra lépve megvizsgáljuk a 3-as csúcsot, amely már bejárt csúcs. Ezután az előzőhöz hasonlóan még megvizsgáljuk a maradék 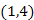él mentén a 4-es csúcsot, de annak színe sem fehér. Az 1-esből kimenő összes él mentén megvizsgáltuk a továbblépési lehetőségeket, így az 1-es csúcsot utolsóként elhagyva befejeztük a bejárást.

Vissza a tartalomjegyzékhez

28.3. A mélységi bejárás algoritmusa

Legyen 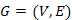irányított vagy irányítatlan véges gráf, ahol 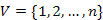. Továbbá, definiáljuk az alábbi tömböket:

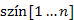• : az ADS szintű színezés megvalósítására;
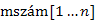• és 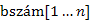: az ADS szinten említett mélységi és befejezési számok nyilvántartására;
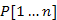• : a bejárás során, egy csúcs megelőző csúcsának a nyilvántartására (a korábban látottakhoz hasonlóan, lásd például: szélességi bejárás vagy Dijkstra-algoritmus).

Az előző példában úgy kezdtük a bejárást, hogy kijelöltünk egy kezdőcsúcsot, amelyből kiindulva történetesen az összes csúcs elérhető volt mélységi bejárással. Egy másik példában előfordulhatna, hogy lennének olyan csúcsok, amelyeket egyáltalán nem tudnánk elérni egy kiválasztott startcsúcsból. A későbbi alkalmazások érdekében a mélységi bejárást úgy definiáljuk, hogy az a gráf minden pontjához eljusson.

Az algoritmus működésének nem feltétele egy kezdőcsúcs megadása, azt az eljárás keretében magunk tetszőlegesen választjuk meg, kívülről nézve véletlen jelleggel. Miután minden, ebből elérhető csúcsot bejártunk, visszajutottunk az említett kezdőpontba. Ha maradt olyan csúcs, amelyet a bejárás nem ért el, azaz színe fehér maradt, akkor választunk közülük egy következőt és abból kiindulva újra elvégezzük a mélységi bejárást.

Ezt az eljárást addig folytatjuk, amíg van fehér csúcsunk. Nyilván minden ilyen menetben legalább egy csúcsot átszínezünk feketére, tehát véges számú menet után elfogynak a fehér csúcsok. Elegendő a csúcsok halmazán egyszer végigmenni (a gyakorlatban a csúcsok címkéje szerinti növekedően), és ha egy csúcs színe fehér, akkor onnan indítsunk egy bejárást.

Tehát az algoritmust bontsuk két részre, vagy inkább két szintre. Az egyik szintet az a rekurzív „belső” algoritmus valósítja meg (lásd: 28.6. ábra), amely egy megadott kezdőcsúcsból indítja a bejárást, ez lesz az 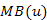eljárás. A másik, „külső” algoritmus, (lásd: 28.5. ábra) végigveszi a gráf pontjait, és minden fehér csúcsra elindítja az előbbi eljárást.

Az pontból induló 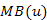mélységi bejárásra egyszerű rekurzív definíciót adni, amely szerint az u csúcsot pontosan akkor jártuk be, ha az összes szomszédját bejártuk. Ennek alapján az 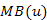eljárást rekurzív formában adjuk meg. A rekurzív eljárás önmagát hívja meg egy csúcs szomszédjaira, azzal a „kijárattal”, hogy csak fehér színű csúcs esetén történik hívás.

A kép (nagyobb változata) külön ablakban is megtekinthető.fej28_24_full.png28.5. ábra. A mélységi bejárás "külső" algoritmusa

A kép (nagyobb változata) külön ablakban is megtekinthető.fej28_25_full.png28.6. ábra. A mélységi bejárás "belső" algoritmusa

Az 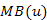eljárás futása során feljegyezzük a P tömbbe egy csúcs megelőzőjét, így egy u csúcsból kiinduló, úgynevezett mélységi feszítőfát kapunk. A 28.1. fejezet példáján az 1-es csúcsból kiinduló mélységi faként a 28.7. ábrán látható gráfot kapjuk. Összességében, pedig a P tömbben feljegyzett megelőzési reláció, G egy- esetleg több fából álló – részgráfját adja, amelyet mélységi erdőnek nevezünk.

Definíció. Legyen G=(V,E) irányított, véges gráf. A G mélységi bejárása után a P-ben keletkező megelőzési reláció által ábrázolható irányított T részgráfot, a G gráf egy mélységi erdőjének nevezzük.

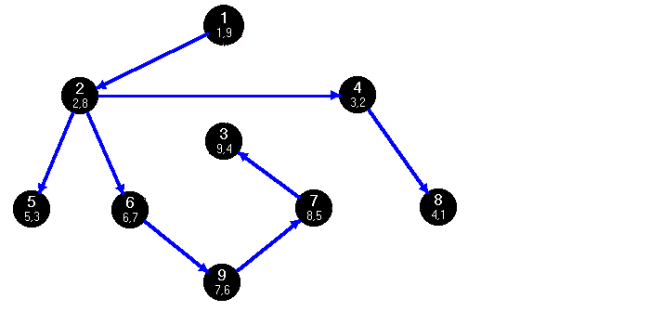A kép (nagyobb változata) külön ablakban is megtekinthető.fej28_26_full.png28.7. ábra. A mélységi erdő

A mélységi bejárás műveletigényének meghatározásakor elegendő azt figyelembe venni, hogy egyrészt minden u csúcsra pontosan egyszer hívjuk meg az MB(u) eljárást, másrészt az eljárásban a csúcsnak minden szomszédját vizsgáljuk, ami összesen annyi vizsgálatot jelent, mint ahány éle van a gráfnak, így

Vissza a tartalomjegyzékhez

28.4. Élek osztályozása a mélységi bejárás szerint

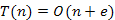
A mélységi bejárás során felfedezett éleket különböző kategóriákba sorolhatjuk. Ezek ismertetése előtt azonban tisztáznunk kell néhány alapfogalmat és állítást.

Definíció. Legyen T a G=(V,E) gráf egy mélységi erdője, és 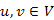csúcsok. A v leszármazottja u-nak T -ben, ha 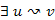T-beli irányított út.

Állítás. (a leszármazottság szükséges feltétele): Legyen T a G=(V,E) gráf egy mélységi erdője, 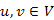csúcsok, 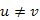, és v leszármazottja u-nak T -ben, akkor
.

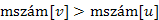Bizonyítás. Tegyük fel, hogy v leszármazottja u-nak T -ben, tehát 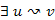út T-ben. Ez az út úgy keletkezik, hogy az út 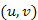éleinek vizsgálatakor, 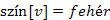csúcsok esetén a P tömbbe bejegyzésre kerül a megelőző u csúcs, majd meghívjuk az 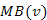eljárást, ahol a v csúcs legalább egyel megnövelt mélységi szám értéket fog kapni.

Állítás. (leszármazottság szükséges és elégséges feltétele): Legyen T a G=(V,E) gráf egy mélységi erdője, 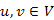csúcsok, 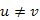. Ekkor 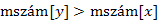és
akkor, és csak akkor, ha v leszármazottja u-nak T -ben.

Bizonyítás. A mélységi és befejezési számok viszonyából következik, hogy előbb meghívtuk az 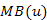eljárást, majd még mielőtt végett ért volna az u szomszédainak rekurzív bejárását végző ciklus, meghívtuk 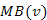-t, amely teljes egészében lefutott, majd csak ez után terminálhatott az említett ciklus. Ez akkor lehetséges, ha létezik egy olyan csúcs, hogy az eljárásban hívtuk meg 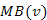-ot, és 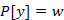bejegyzésre kerül. Továbbá a w csúcs olyan, hogy 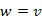(azaz w szomszédja u-nak) vagy lefutása is teljesül, amit az 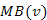-ról az előbb említettünk. Ezt a gondolatmenetet addig folytathatjuk, míg 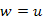nem lesz, miközben láthatjuk, hogy a P tömb bejegyzései által reprezentált irányított úton haladunk visszafelé (a rekurzív hívási fán haladunk felfelé). Tehát ez az út igazolja, hogy v leszármazottja u-nak T -ben.

Állítás. (Fehér út tétel): Legyen T a G=(V,E) gráf egy mélységi erdője, 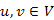csúcsok,
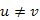. Ekkor v leszármazottja u-nak T -ben akkor, és csak akkor, ha u elérésekor a v elérhető az u-ból, az u kivételével csak fehér csúcsokat tartalmazó úton.

Bizonyítás.

: Legyen v leszármazottja u-nak. Ekkor 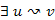T-beli út, amelynek mentén minden csúcs leszármazottja u-nak. Ezen fabeli út minden w csúcsára teljesül, hogy 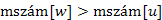, azaz minden w csúcsot később érünk el, mint az u-t. Tehát az u elérésekor a w leszármazott csúcsok még fehérek.

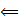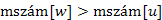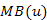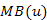: Tegyük fel, hogy u elérésekor létezik v -be vezető fehér csúcsokból álló út, legyen w egy ilyen út első olyan csúcsa, amelyet az u szomszédait felsoroló ciklusban elérünk, azaz meghívjuk az eljárást. Az u csúcs már szürke és még fehér, ezért w-t később érjük el, mint u-et, tehát . Továbbá belsejéből hívtuk meg -t tehát előbb lefut, mint , azaz . Tehát a korábbi állítás szerint w leszármazottja u-nak. Azonban feltettük, hogy w-t érjük el először az v -hez vezető úton, tehát az út többi csúcsa v elérésekor még fehér, így a 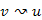útra hasonlóan alkalmazható a fenti rekurzív gondolatmenet (míg el nem jutunk az 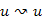útig). Miután beláttuk, hogy w leszármazottja u-nak és v leszármazottja w-nek, tehát v leszármazottja u-nak.

Megjegyzés. Ha 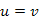, akkor triviálisan teljesül a kölcsönös leszármazottság.

A leszármazott fogalmát kihasználva az éleket a következő osztályokba sorolhatjuk a mélységi bejárás szerint. Legyen T a G=(V,E) gráf egy mélységi erdője, és 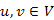csúcsok. Az 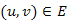él

1.faél, ha 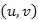éle T-nek;

2.előreél, ha 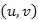nem éle T-nek, de v leszármazottja u-nak T-ben, és ;

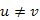3.visszaél, ha u leszármazottja v-nek T-ben (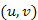 nem éle T-nek, ide tartozik 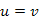hurokél is);

4.keresztél, ha u és v nem leszármazottai egymásnak T-ben.

Az éltípusokat az eljárás végrehajtása közben tudjuk megállapítani, az mszám és bszám, értékek segítségével, ahogy az állítások esetében láttuk.

Állítás. Tegyük fel, hogy G=(V,E) irányított véges gráf mélység bejárása során éppen az 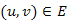vizsgálatánál tartunk. Ekkor 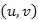él

1.faél, ha ;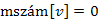

2.előreél, ha ;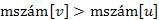

3.visszaél, ha 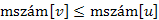és ;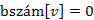

4.keresztél, ha 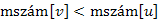és .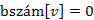

Bizonyítás

1.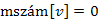 azt jelenti, hogy most érjük el a v csúcsot, azaz a csúcs még fehér. Továbbá az 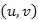él mentén jutunk az v csúcsba, mint u szomszédja, amely az 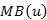u szomszédait felsoroló ciklusában, az elágazás bal oldali ágában lehetséges, ahol valóban a P tömbbe bejegyzésre kerül az él, tehát faél lesz.

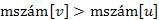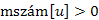2. és , így 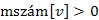, tehát v nem fehér (így az él nem lehet faél). Továbbá a mélységi számok viszonyából következik, hogy az 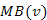-t később hívtuk meg, mint az 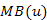-t, de az 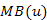még nem fejeződött be. Így az 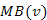meghívása, az 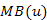eljárás u szomszédait felsoroló ciklusában, valamely szomszédra meghívott MB eljárásban, vagy annak rekurzív leszármazottjában történt, az 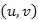él vizsgálata előtt. Azonban az 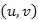él vizsgálata a ciklus egy későbbi iterációjában történik, tehát az 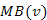-nek mostanra be kellet fejeződnie, de az 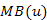még csak ezek után fog befejeződni .

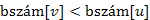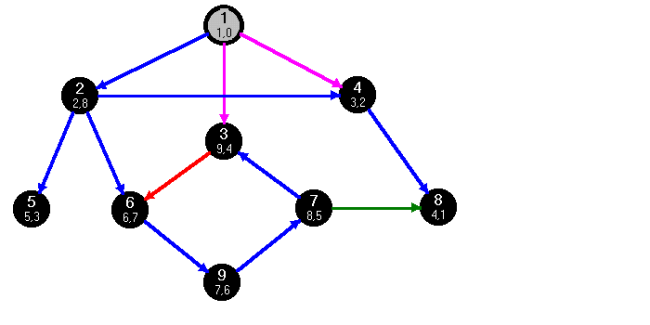A kép (nagyobb változata) külön ablakban is megtekinthető.fej28_22_full.png28.8. ábra. Előreél detektálása (rózsaszínnel jelölve)

Korábbi állításunkat felhasználva beláthatjuk, hogy v leszármazottja u-nak T-ben, és láttuk, hogy nem lehet faél, tehát előreél. Láthatjuk a 28.1. fejezetben vizsgált példán, hogy az 1-es csúcsból a 3-as csúcsba vezető él feldolgozásakor a 3-as csúcshoz már eljutottunk az 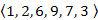úton. Tehát a 3-as leszármazottja az 1-nek, és az 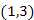él nem faél, tehát előreél (28.8. ábra).

3.Ha 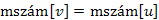, akkor 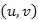hurokél, ami triviálisan visszaél. Ha 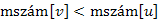és 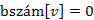, akkor a v bejárása elkezdődött, de még nem fejeződött be. Elkezdtük az u bejárását, amelynek során vizsgáljuk az 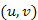élt. Tehát az v bejárása során jutunk el az u-hoz, azaz u leszármazottja v -nek. Az 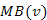eljárásban, vagy annak valamely rekurzív leszármazottjában hívtuk meg az 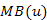-t, tehát az 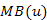-nak előbb kell befejeződnie, mint az 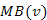-nek. A 28.9. ábrán a 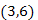él visszaél.

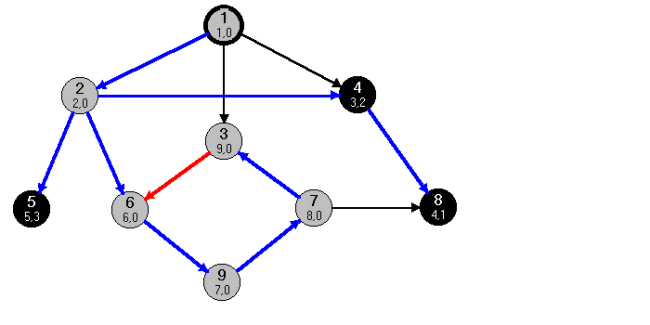A kép (nagyobb változata) külön ablakban is megtekinthető.fej28_14_full.png28.9. ábra. Visszaél detektálása (piros színnel jelölve)

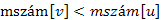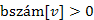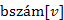4. szükséges feltétele, hogy u leszármazottja legyen v -nek, de az v bejárása befejeződött (), míg az u bejárása még nem, tehát a csak nagyobb lehet -nél, azaz az elégséges feltétel nem teljesül. Tehát u és v nem leszármazottai egymásnak T-ben, amiből következik, hogy 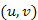él keresztél. A 28.10. ábrán a (7,8) élt, mint keresztélt detektáltuk.

A kép (nagyobb változata) külön ablakban is megtekinthető.fej28_16_full.png28.10. ábra. Keresztél detektálása (zöld színnel jelölve)

Vissza a tartalomjegyzékhez

28.5. A mélységi bejárás egy illusztrációja

Az alábbi „pillanatfelvételek” inkább az idézett irodalmi leírás illusztrálásához készültek, minthogy a gráfos algoritmus működést részletesen egy másik ábrasoron mutattuk be.

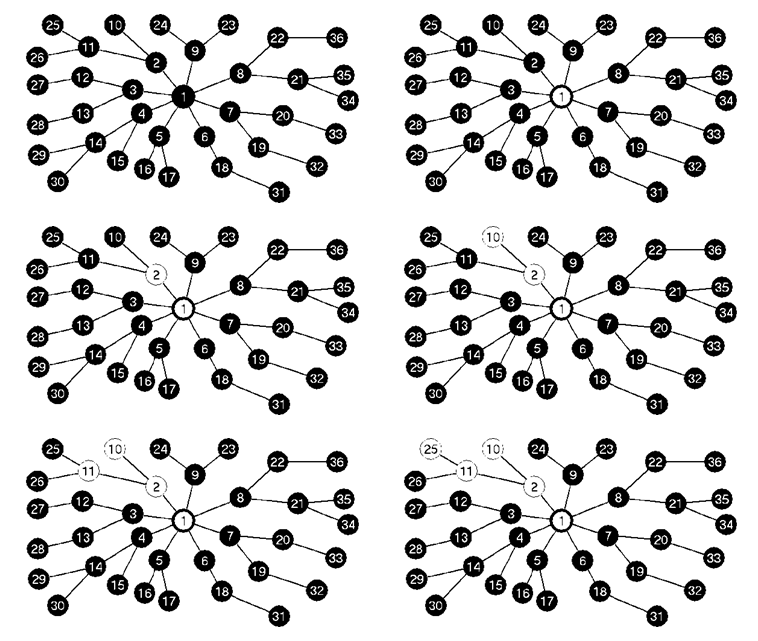
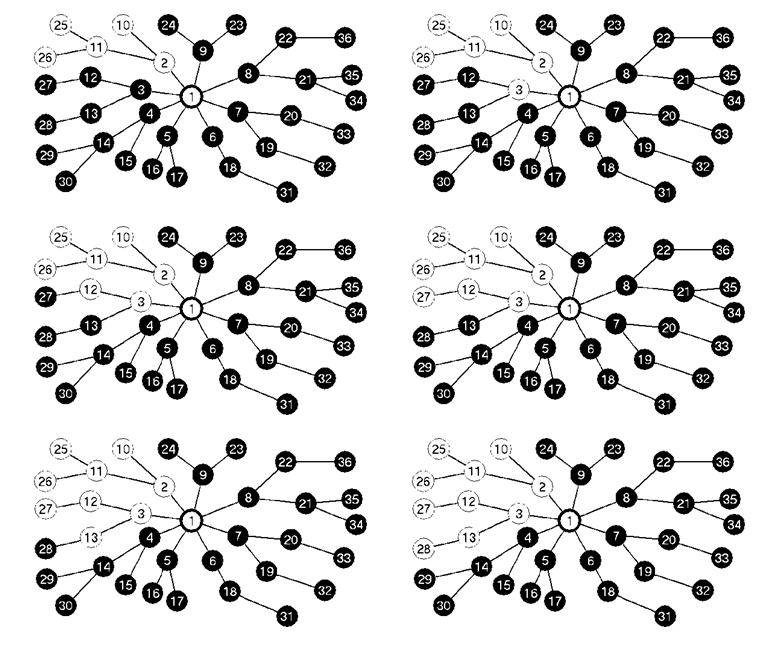
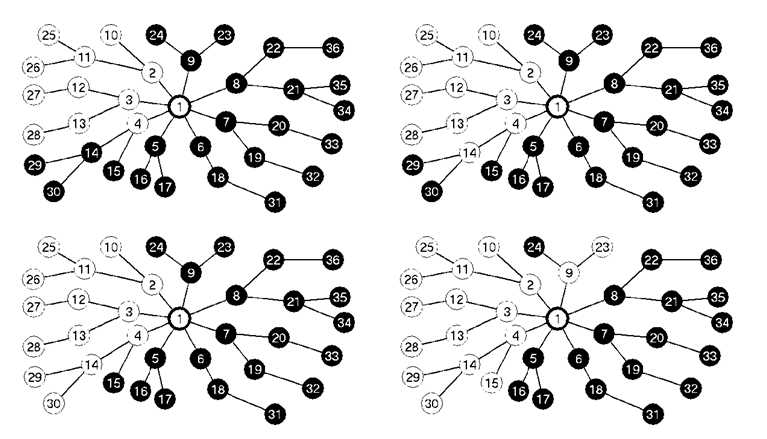
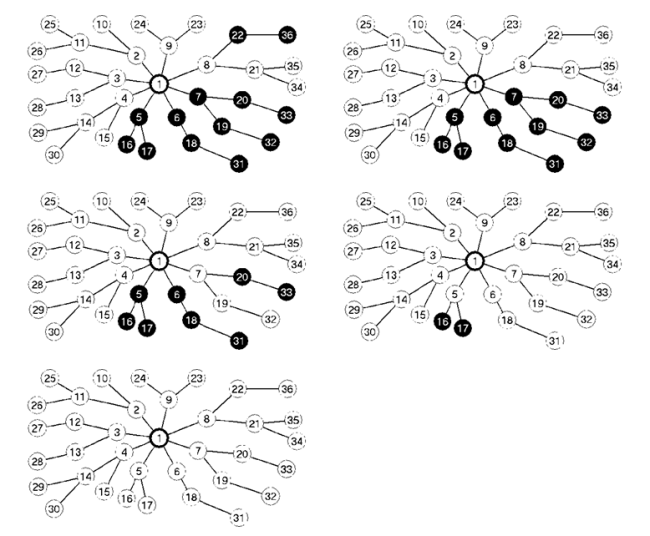A kép (nagyobb változata) külön ablakban is megtekinthető.fej28_s8_full.png28.11. ábra. Mélységi bejárás egy gráfon (illusztráció a "kisváros lámpáihoz")

Vissza a tartalomjegyzékhez