Az ismertetésre kerülő adatszerkezeteket és algoritmusokat mindig jellemezzük majd a hatékonyság szempontjából. Az adatszerkezetek egyes ábrázolásairól megállapítjuk a helyfoglalásukat, az algoritmusoknál pedig a műveletigényt becsüljük, mindkettőt az input adatok méretének függvényében. Általában megelégszünk mindkét adat nagyságrendben közelítő értékével. A nagyságrendi értékek közelítő ereje annál nagyobb, minél nagyobb méretű adatokra értelmezzük azokat. Amint látjuk majd, egy sajátos matematikai határérték-fogalmat vezetünk be és alkalmazunk a hatékonyságra irányuló számításainkban.
A műveletigény számításakor eleve azzal a közelítéssel élünk, hogy csak az algoritmus meghatározó műveleteit vesszük számításba. Egy műveletet meghatározónak (dominánsnak) mondunk, ha a többihez képest jelentős a végrehajtási ideje, valamint a végrehajtásainak száma. Általában kijelölhető egyetlen meghatározó művelet, amelyre a számítást elvégezzük. A műveletigényt a kiszemelt művelet végrehajtásainak számával adjuk meg, mivel az egyes műveletek végrehajtási ideje gépről-gépre változhat. A lépésszám közelítéssel kiszámolt nagyságrendje – gyakorlati tapasztalatok szerint is – jól jellemzi az algoritmus tényleges futási idejét.
A rendezés általános feladata jól ismert. A tömbökre megfogalmazott változat egyik legkorábbi (kevéssé hatékony) megoldása a buborékrendezés. Az eljárás működésének alapja a szomszédos elemek cseréje, amennyiben az elől álló nagyobb, mint az utána következő. Az első menetben a szomszédos elemek cseréjével „felbuborékoltatjuk” a legnagyobb elemet a tömb végére. A következő iterációs lépésben ugyanezt tesszük az „eggyel rövidebb” tömbben, és így tovább. Utoljára még a tömb első két elemét is megcseréljük, ha szükséges. Az (n–1)-edik iteráció végére elérjük, hogy az elemek nagyság szerint növekvő sorban követik egymást. A rendezés algoritmusa az 1.1. ábrán látható. (Az egyszerűség kedvéért a Csere műveletét nem bontottuk három értékadásra.)
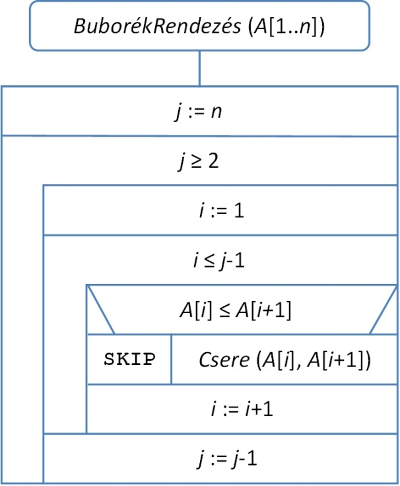 fej1_001_full.png1.1. ábra. A buborékrendezés algoritmusa
fej1_001_full.png1.1. ábra. A buborékrendezés algoritmusaAz algoritmus műveleteit két kategóriába sorolhatjuk. Az egyikbe tartoznak a ciklusváltozókra vonatkozó műveletek, a másikba pedig az A[1..n] tömb szomszédos elemeinek összehasonlítása és cseréje. Nyilvánvaló, hogy az utóbbiak a meghatározó műveletek. Egyrészt végrehajtásuk lényegesen nagyobb időt vesz igénybe, mint a ciklust adminisztráló utasításoké (különösen, ha a tömb elemeinek mérete jelentős), másrészt mindkét utasítás a belső ciklusban van (még ha a csere feltételhez kötött is), így végrehajtásukra minden iterációs lépésben sor kerülhet. Ezért az összehasonlítások, illetve a cserék számát fogjuk számolni. Ha ezt a döntést meghoztuk, érdemes az algoritmusban szereplő ciklusokat tömörebb, áttekinthetőbb formában, for-ciklusként újra felírni. Ez a változat látható az 1.2. ábrán.
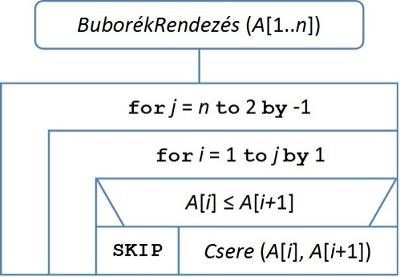 fej1_002_full.png1.2. ábra. Buborékrendezés (for-ciklusokkal)
fej1_002_full.png1.2. ábra. Buborékrendezés (for-ciklusokkal)A számolást az egyszerűség kedvéért külön-külön végezzük. Nézzük először az összehasonlítások Ö(n)-nel jelölt számát. A külső ciklus magja (n–1)-szer hajtódik végre, a belső ciklus ennek megfelelően rendre n–1, n–2, ..., 1 iterációt eredményez. Mivel a két szomszédos elem összehasonlítása a belső ciklusnak olyan utasítása, amely mindig végrehajtódik, ezért
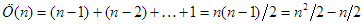
Az 1.3. pontban precízen bevezetjük majd azokat az aszimptotikus fogalmakat és jelöléseket, amelyekkel a műveletigény nagyságrendjét jellemezzük. Most elégedjünk meg annyival, hogy általában elegendő az, ha csak a kifejezés domináns nagyságrendű tagját tartjuk meg, az együttható elhagyásával. Az összehasonlítások számára ennek megfelelően azt mondjuk majd, hogy értéke nagyságrendben n2 és ezt így jelöljük:
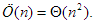
Megjegyezzük, hogy az összehasonlítások száma a bemenő adatok bármely permutációjára ugyanannyi. Az elemzett műveletek végrehajtási száma a legtöbbször azonban változó az adatok függvényében. Ilyenkor elsősorban a végrehajtások maximális és átlagos számára vagyunk kíváncsiak, de a minimális végrehajtási számot is gyakran meghatározzuk, bár ennek általában nincs jelentősége. Ha T(n)-nel jelöljük a műveletigényt, akkor annak minimális, maximális és átlagos értékét rendre mT(n), MT(n) és AT(n) jelöli.
Vizsgáljuk meg most a cserék Cs(n)-nel jelölt számát. Ez a szám már nem állandó, hanem a bemenő adatok függvénye. Nevezetesen, a cserék száma megegyezik az A[1..n] tömb elemei között fennálló inverziók számával:
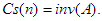
Valóban, minden csere pontosan egy inverziót szüntet meg a két szomszédos elem között, újat viszont nem hoz létre. A rendezett tömbben pedig nincs inverzió. Ha a tömb eleve rendezett, akkor egyetlen cserét sem kell végrehajtani, így a cserék száma a legkedvezőbb esetben nulla, azaz
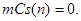
A legtöbb cserét akkor kell végrehajtani, ha minden szomszédos elempár inverzióban áll, azaz akkor, ha a tömb éppen fordítva, nagyság szerint csökkenő módon rendezett. Ekkor
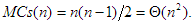
A cserék átlagos számának meghatározásához először is feltesszük, hogy a rendezendő számok minden permutációja egyformán valószínű. (Az átlagos műveletigény számításához mindig ismerni kell a bemenő adatok valószínűségi eloszlását, vagy legalább is feltételezéssel kell élni arra nézve!) Az általánosság megszorítása nélkül vehetjük úgy, hogy az 1, 2, ..., n számokat kell rendeznünk, ha elfogadjuk azt a szokásos egyszerűsítést, hogy a rendezendő értékek mind különbözők.
A cserék számának átlagát nyilvánvalóan úgy kapjuk, hogy az 1, 2, ..., n elemek minden permutációjának inverziószámát összeadjuk és osztjuk a permutációk számával:
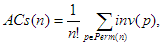
ahol Perm(n) az n elem összes permutációinak halmazát jelöli. Az összeg meghatározásánál nehézségbe ütközünk, ha megpróbáljuk azt megmondani, hogy adott n-re hány olyan permutáció van, amelyben i számú inverzió található (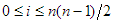 ). Ehelyett célszerű párosítani a permutációkat úgy, hogy mindegyikkel párba állítjuk az inverzét, pl. az p=1423 és a pR=3241 alkot egy ilyen párt. Egy ilyen párban az inverziók száma együtt éppen a lehetséges
). Ehelyett célszerű párosítani a permutációkat úgy, hogy mindegyikkel párba állítjuk az inverzét, pl. az p=1423 és a pR=3241 alkot egy ilyen párt. Egy ilyen párban az inverziók száma együtt éppen a lehetséges 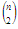 -t teszi ki, pl.
-t teszi ki, pl. 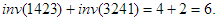 Az állítás igazolására gondoljuk meg, hogy egy permutációban két elem pontosan akkor áll inverzióban, hogy ha az inverz permutációban nincs közöttük inverzió. Írjuk le gondolatban mind az n! permutációt kétszer egymás mellé egy-egy oszlopba, a mondott párosításnak megfelelően. Ekkor minden sorban a két permutáció inverzióinak száma együtt
Az állítás igazolására gondoljuk meg, hogy egy permutációban két elem pontosan akkor áll inverzióban, hogy ha az inverz permutációban nincs közöttük inverzió. Írjuk le gondolatban mind az n! permutációt kétszer egymás mellé egy-egy oszlopba, a mondott párosításnak megfelelően. Ekkor minden sorban a két permutáció inverzióinak száma együtt 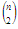 , így
, így
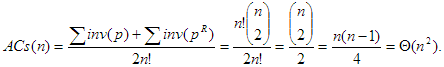
A cserék számának átlaga tehát a legnagyobb érték fele, de nagyságrendben ez így is n2-es.
Az elemzés eredménye az, hogy a buborékrendezés a legrosszabb és az átlagos esetben is – mindkét meghatározó művelete szerint – nagyságrendben n2-es algoritmus.
A következő algoritmus, amelyet elemzünk, a Hanoi tornyai probléma megoldása. A probléma régről ismert. Adott három rúd és az elsőn n darab, felfelé egyre csökkenő méretű korong, ahogyan az 1.3. ábrán látható n=4 esetére.
A feladat az, hogy a korongokat át kell helyezni az A rúdról a B-re, a C rúd felhasználásával, oly módon, hogy egyszerre csak egy korongot szabad mozgatni és csak nála nagyobb korongra, vagy üres rúdra lehet áthelyezni.
A feladatnak több különböző megoldása van, köztük olyan (iteratív) heurisztikus algoritmusok, amelyek a mesterséges intelligencia területére tartoznak. Itt a szokásos rekurzív algoritmust ismertetjük.
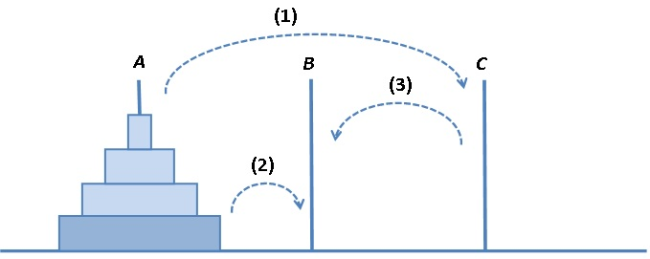 fej1_013_full.png1.3. ábra. Hanoi tornyai probléma
fej1_013_full.png1.3. ábra. Hanoi tornyai problémaSzámítógépes programok, algoritmusok esetén akkor beszélünk rekurzióról, hogyha az adott eljárás a működése során „meghívja önmagát”, vagyis a számítás egyik lépéseként önmagát hajtja végre, más bemeneti adatokkal, paraméterekkel.
Sok hasznos algoritmus rekurzív szerkezetű, és többnyire az ún. „oszd meg és uralkodj” elv alapján működnek. Ennek a lényege az, hogy a feladatot több részfeladatra bontjuk, amelyek egyenként az eredetihez nagyon hasonlóak, de kisebb méretűek, így könnyebben megoldhatók. A definiált működésnek az lesz a hatása, hogy a részfeladatokat hasonlóan, további egyre kisebb és kisebb részekre osztja az eljárás, amíg el nem éri az elemei feladatok megadott méretét. A már kellően kicsi részfeladatokat közvetlen módon megoldjuk. Ez az elemi lépés gyakran egészen egyszerű. Ezután a rekurzív hívások rendszerében „visszafelé” haladva minden lépésben összegezzük, összevonjuk a részfeladatok megoldását. Az utolsó lépésben, amikor a működés visszaér a kiinduló szintre, megkapjuk az eredeti feladat megoldását.
A módszer általános elnevezése onnan ered, hogy a rekurzió minden szintjén három alapvető lépést hajt végre:
Ennek az általános elvnek megfelelően a Hanoi tornyai probléma rekurzív megoldási elve a következő:
1. A felső n–1 korongot helyezzük át az A rúdról a C-re a megengedett lépésekkel úgy, hogy a B rudat vesszük segítségül. (Ez az eredetihez hasonló, de kisebb méretű feladat.)
2. Az egyedül maradt alsó korongot tegyük át az A rúdról az üres B-re. (Ez az elemi méretű feladat közvetlen megoldása.)
3. Vigyük át a C rúdon található n–1 korongot a B-re az A rúd igénybe vételével, hasonlóan ahhoz, ahogyan az 1. pontban eljártunk.
A rekurzív eljárás működése 1. és 3. lépésben szereplő n–1 korongot hasonló szemlélettel n–2 korong kétszeri mozgatására, valamint egy korong áthelyezésére bontja, és így tovább.
A rekurzióból való "kijárat" megfogalmazása természetes módon egyetlen korongra adódna: ha n=1, akkor egyszerűen tegyük át a korongot a rendeltetési helyére. Egyszerűbb formájú algoritmust kapunk, amelyet elemezni is könnyebb, ha "még lejjebb" adjuk meg a kijáratot a rekurzióból: ha n=0, akkor nem kell semmit sem tennünk. Erre az ad lehetőséget, hogy így az n=1 eset is kezelhető a fenti három lépéssel: az 1. és a 3. lépés üressé válik, a 2. lépés pedig tartalmazza az elemi áthelyezés műveletét.
Általános szabályként jegyezzük meg azt, hogy a rekurzióból való kijáratot „engedjük minél lejjebb”, azaz a szóban forgó változó minél kisebb értékére próbáljuk azt megadni (pl. a kínálkozó n = 1 helyett az n = 0 esetre). Arra törekszünk tehát, hogy minél kisebb legyen az a részfeladat, amelyet már közvetlenül oldunk meg.
Írjuk meg ezután az eljárást! A Hanoi(n,i,j,k) rekurzív eljárás n számú korongot átvisz az i-edik rúdról a j-edikre, a k-adik rúd felhasználásával. Az eljárást "kívülről" a konkrét feladatnak megfelelő paraméterekkel kell meghívni, pl. az ábrán látható esetben így: Hanoi(4,1,2,3). Az eljárás struktogramja a 1.4. ábrán látható. A rekurzív eljárás önmagát hívja egészen addig, amíg n nagyobb nullánál. Amikor n=1, akkor is ez történik, de a rekurzív hívások végrehajtása az n=0 ágon már egy-egy üres utasítást eredményez. Az Átrak(i,j) utasítás jelöli azt az elemi műveletet, amellyel egyetlen korongot átteszünk az i-edik rúdról a j-edikre.
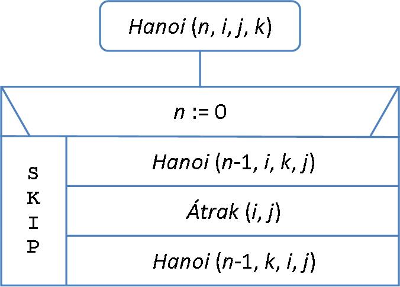 fej1_014_full.png 1.4.ábra. A Hanoi tornyai probléma megoldása
fej1_014_full.png 1.4.ábra. A Hanoi tornyai probléma megoldásaMeghatározzuk az n korong átpakolásához szükséges lépésszámot. Az algoritmus rekurzív megfogalmazása szinte kínálja az átrakások számára vonatkozó rekurzív egyenletet:
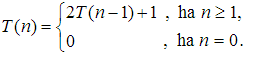
Ha kiszámítjuk T(n) értékét néhány n-re, akkor azt sejthetjük, hogy 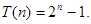 Ezt teljes indukcióval könnyen bebizonyíthatjuk. Azt kaptuk, hogy a Hanoi tornyai egy exponenciális műveletigényű probléma:
Ezt teljes indukcióval könnyen bebizonyíthatjuk. Azt kaptuk, hogy a Hanoi tornyai egy exponenciális műveletigényű probléma: 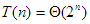 .
.
(A legenda szerint Indiában, egy ősi város templomában a szerzetesek ezt a feladatot 64 korongra kezdték el valamikor megoldani azzal, hogy amikor a rakosgatás végére érnek, elkövetkezik a világ vége. Ha minden korongot 1 mp alatt helyeznek át, akkor a 64 korong teljes átpakolása nagyságrendben 600 milliárd évet venne igénybe. Ha 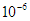 mp-cel számolunk, ami már a számítógépek sebessége, akkor is nem egészen 600 ezer évre lenne szükség a korongok átrendezéséhez. A nagyságrendek érzékeltetésére: az univerzumról úgy tudjuk, hogy kevesebb, mint 14 milliárd éves, a másodiknak kiszámolt időtartam pedig a homo sapiens megjelenése óta eltelt idővel egyezik meg nagyságrendben.)
mp-cel számolunk, ami már a számítógépek sebessége, akkor is nem egészen 600 ezer évre lenne szükség a korongok átrendezéséhez. A nagyságrendek érzékeltetésére: az univerzumról úgy tudjuk, hogy kevesebb, mint 14 milliárd éves, a másodiknak kiszámolt időtartam pedig a homo sapiens megjelenése óta eltelt idővel egyezik meg nagyságrendben.)
Azt javasoljuk, hogy az olvasó ne tekintse befejezettnek alapszintű tanulmányait az algoritmusok témakörében, amíg ezzel az alfejezettel meg nem ismerkedett! Célszerű most átolvasni ezt a *-gal jelölt 1.3. részt, majd később – talán többször is – visszatérni ide a mélyebb megértés céljával.
Kiszámítottuk két algoritmus műveletigényét a bemenő adatok méretének függvényében. Szeretnénk pontosabb matematikai fogalmakra támaszkodva beszélni az algoritmusok hatékonyságáról. Ebben a pontban ennek megalapozása történik. Először is alkalmasan megválasztjuk az algoritmusok műveletigényét, illetve lépésszámát jelentő függvények értelmezési tartományát és értékkészletét.
A továbbiakban legyen f olyan függvény, amelyet a természetes számok halmazán értelmezünk és nem-negatív valós értékeket vesz fel:
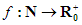 , ahol
, ahol 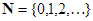 .
.
Definiáljuk egy adott g függvény esetén azon függvények osztályait, amelyek nagyságrendben rendre nem nagyobbak, kisebbek, nem kisebbek, nagyobbak, mint g, illetve g-vel azonos nagyságrendűek. Az osztályok jelölései és nevei: O „nagy ordó” vagy „ordó”, 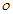 ”kis ordó”,
”kis ordó”, 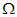 „nagy omega”,
„nagy omega”, 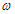 „kis omega” és
„kis omega” és 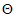 theta.
theta.
1. adott g függvény esetén O(g)-vel jelöljük függvényeknek azt a halmazát, amelyre
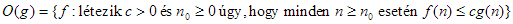
teljesül. Ha 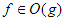 , akkor azt mondjuk, hogy g aszimptotikus felső korlátja f-nek. Ebben az esetben szokásos módon inkább az
, akkor azt mondjuk, hogy g aszimptotikus felső korlátja f-nek. Ebben az esetben szokásos módon inkább az 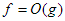 jelölést alkalmazzuk. Valamint, használjuk a következő függvényhalmazt is:
jelölést alkalmazzuk. Valamint, használjuk a következő függvényhalmazt is:
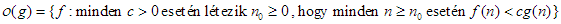
2. Hasonlóan, jelölje  azon függvények halmazát, amelyekre
azon függvények halmazát, amelyekre
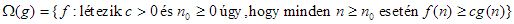
áll fenn. Ha 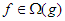 – szokásos jelöléssel
– szokásos jelöléssel 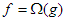 –, akkor azt mondjuk, hogy g aszimptotikus alsó korlátja f-nek. Az itt megjelenő másik függvényhalmaz pedig:
–, akkor azt mondjuk, hogy g aszimptotikus alsó korlátja f-nek. Az itt megjelenő másik függvényhalmaz pedig:
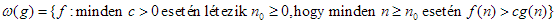
3. Végül, 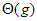 jelöli azt a függvényosztályt, amelyet a
jelöli azt a függvényosztályt, amelyet a
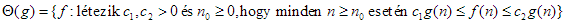 összefüggés ír le. Ha
összefüggés ír le. Ha 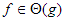 – szokásos jelöléssel
– szokásos jelöléssel  –, akkor azt mondjuk, hogy g aszimptotikusan éles korlátja f-nek.
–, akkor azt mondjuk, hogy g aszimptotikusan éles korlátja f-nek.
A definíciók alapján teljesül a következő egyenlőség: 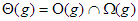 .
.
Ha egy tetszőleges, rögzített g függvényt tekintünk, akkor a többi függvény általában besorolható a most definiált osztályok némelyikébe. (Megjegyezzük, hogy vannak nem összehasonlítható függvények is, pl. 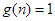 és
és 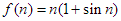 , ill.
, ill. 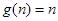 és
és  minden n-re. Könnyen belátható ezekre, hogy sem
minden n-re. Könnyen belátható ezekre, hogy sem 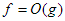 , sem pedig
, sem pedig 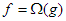 nem teljesül.) A nagyságrendi viszonyokról az 1.5. ábra ad szemléletes képet.
nem teljesül.) A nagyságrendi viszonyokról az 1.5. ábra ad szemléletes képet.
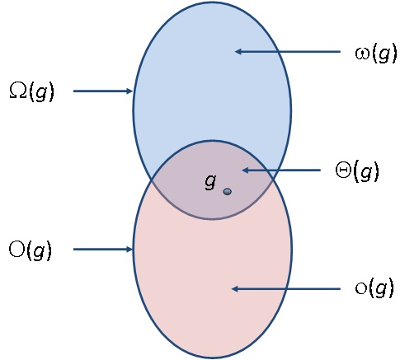 fej1_045_full.png1.5. ábra. A függvényosztályok egymáshoz való viszonya
fej1_045_full.png1.5. ábra. A függvényosztályok egymáshoz való viszonyaA függvények aszimptotikus viszonyainak jelen vizsgálatához az szolgál alapul, hogy kellően nagyméretű bemenet esetén egy algoritmus futási idejének (ill. az azt leíró függvénynek) csak a nagyságrendje lényeges. Viszonylag kisméretű bemeneteket leszámítva tehát az aszimptotikusan leghatékonyabb algoritmus lesz a ténylegesen leggyorsabb!
Valamely adott f és g függvény aszimptotikus viszonyát a 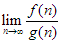 határérték – amennyiben létezik – a következőképpen határozza meg:
határérték – amennyiben létezik – a következőképpen határozza meg:
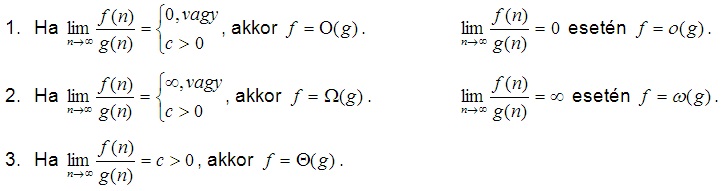
Megjegyzés: A 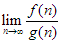 határérték általában létezik, de pl. ha
határérték általában létezik, de pl. ha
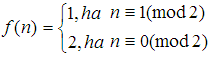
és g(n)=1 minden n-re, akkor nem létezik a határérték, de a két függvény aszimptotikus viszonya mégis megállapítható, ebben az esetben 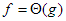 .
.
Ha az adott f és g függvényekre 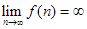 és
és 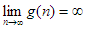 , és mindkét függvény valós kiterjesztése differenciálható, akkor gyakran alkalmazzuk a L’Hospital szabályt a
, és mindkét függvény valós kiterjesztése differenciálható, akkor gyakran alkalmazzuk a L’Hospital szabályt a
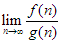 határérték meghatározására:
határérték meghatározására:
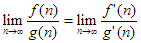
A 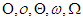 jelöléseket függvények közötti bináris relációként is felfoghatjuk (pl.
jelöléseket függvények közötti bináris relációként is felfoghatjuk (pl.  ). Így a relációkra vonatkozó ismert definíciók értelmezhetők rájuk, és beláthatók a következő állítások:
). Így a relációkra vonatkozó ismert definíciók értelmezhetők rájuk, és beláthatók a következő állítások:
1. 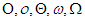 mind tranzitív: f, g, h függvényekre pl.:
mind tranzitív: f, g, h függvényekre pl.: 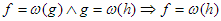 .
.
2.  mindegyike reflexív: pl.
mindegyike reflexív: pl. 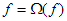 .
.
3.  szimmetrikus:
szimmetrikus: 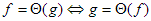 .
.
4. 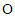 és
és 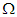 , valamint
, valamint 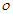 és
és 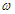 „felcserélten szimmetrikusak: pl.
„felcserélten szimmetrikusak: pl. 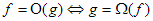 .
.
5. Rögzített h függvény mellett 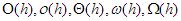 halmazok zártak az összeadásra és a (pozitív) számmal való szorzásra nézve: pl.
halmazok zártak az összeadásra és a (pozitív) számmal való szorzásra nézve: pl. 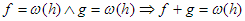 ; és
; és 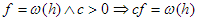 .
.
6. Összegben a nagyobb függvény határozza meg az aszimptotikát: 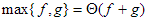 .
.
(Itt a max jelölés az aszimptotikusan nagyobb függvényt jelenti.) Ha ezt a szokásos alakot átírjuk az 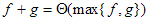 formába, akkor könnyen kiolvasható belőle az, hogy egy szekvencia műveletigényének nagyságrendjét a nagyobb műveletigényű tag határozza meg.
formába, akkor könnyen kiolvasható belőle az, hogy egy szekvencia műveletigényének nagyságrendjét a nagyobb műveletigényű tag határozza meg.
A fenti 1., 2. és 3. tulajdonságok miatt 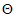 – mint bináris reláció – ekvivalenciareláció a függvények halmazán, tehát osztályokra bontja azt. Az egyes osztályok reprezentálhatók a legegyszerűbb függvényükkel, pl.:
– mint bináris reláció – ekvivalenciareláció a függvények halmazán, tehát osztályokra bontja azt. Az egyes osztályok reprezentálhatók a legegyszerűbb függvényükkel, pl.: 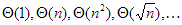
Megjegyzés: A gyakorlatban – amennyiben nem okoz félreértést – az egyszerűség kedvéért a 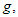
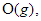

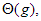
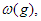
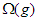 jelölések helyett gyakran a
jelölések helyett gyakran a 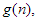

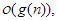
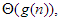

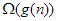 jelöléseket használjuk. Így pl. a
jelöléseket használjuk. Így pl. a 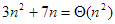 jelentése:
jelentése: 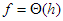 , ahol
, ahol 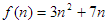 és
és 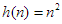 minden n-re.
minden n-re.
Néhány további könnyen belátható tulajdonság:
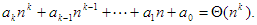
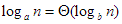 (a>1 és b>1). Ezért az alap feltüntetése nem szükséges:
(a>1 és b>1). Ezért az alap feltüntetése nem szükséges: 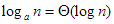
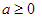 és
és 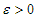 esetén
esetén 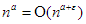 és
és 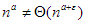 , vagyis
, vagyis 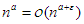 .
.Az aszimptotikus jelölések használatában elterjedt néhány gyakori hiba. Ezek általában nem zavarók, mégis fel kell hívni a figyelmet rájuk. A kritikával azonban már csak azért is óvatosan kell bánni, mert a szerzők egy része kizárólag az 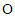 -t használja.
-t használja.
1. Leggyakoribb „hiba” az, hogy algoritmusok műveletigényének jellemzésekor 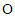 -t használnak, de
-t használnak, de  -t értenek alatta. Az így leírt egyenlőség általában igaz, de mást (kevesebbet) fejez ki, mint amit általában közölni szeretnének általa. Pl. a buborék-rendezésre igaz, hogy
-t értenek alatta. Az így leírt egyenlőség általában igaz, de mást (kevesebbet) fejez ki, mint amit általában közölni szeretnének általa. Pl. a buborék-rendezésre igaz, hogy 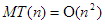 , de többet mond az, hogy
, de többet mond az, hogy 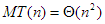 .
.
2. A 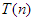 jelölés használata is hibát rejthet.
jelölés használata is hibát rejthet. 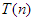 az összes lehetséges futási időt magában foglalja, amelyek nagyságrendben különbözőek lehetnek. Pl. ahogy korábban láttuk, a buborékrendezésre igaz (Cs helyett T-vel), hogy:
az összes lehetséges futási időt magában foglalja, amelyek nagyságrendben különbözőek lehetnek. Pl. ahogy korábban láttuk, a buborékrendezésre igaz (Cs helyett T-vel), hogy: 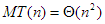 és
és 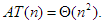 Alegkedvezőbb esetben azonban nincs csere, vagyis
Alegkedvezőbb esetben azonban nincs csere, vagyis 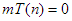 . Ekkor a
. Ekkor a 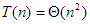 (felületes) kijelentés nem igaz, helyette a
(felületes) kijelentés nem igaz, helyette a 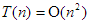 írásmódot kellene használni, mely az összes esetre helyes lesz. Ez azonban kevesebb információt tartalmaz, mint a fenti két egyenlőség, ezért ajánlatos
írásmódot kellene használni, mely az összes esetre helyes lesz. Ez azonban kevesebb információt tartalmaz, mint a fenti két egyenlőség, ezért ajánlatos 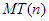 -t és
-t és 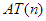 -t használni.
-t használni.
3. Néhány tipikus használat:
a) 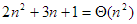 ,
,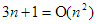 , de
, de 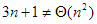
b) 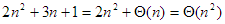
c) A logaritmikus keresés futási idejére fennáll a következő (közelítő) rekurzív egyenlet: 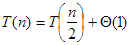 .
.
Néhány jellegzetes, és a gyakorlatban gyakran előforduló függvény menetét és egymáshoz viszonyított aszimptotikus nagyságrendjét szemlélteti az 1.6. ábra (nem mérethűen, főleg nem az origó közelében). Ezek a függvények aszimptotikusan mind különböző nagyságrendűek.
A hatványfüggvények – az ábrán is látható – egyik fontos tulajdonsága, hogy bármely  kitevő esetén
kitevő esetén 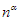 az
az 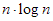 és az
és az 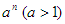 közé, míg ha
közé, míg ha 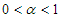 , akkor
, akkor 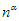 a
a 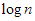 és az
és az 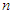 közé esik aszimptotikusan.
közé esik aszimptotikusan.
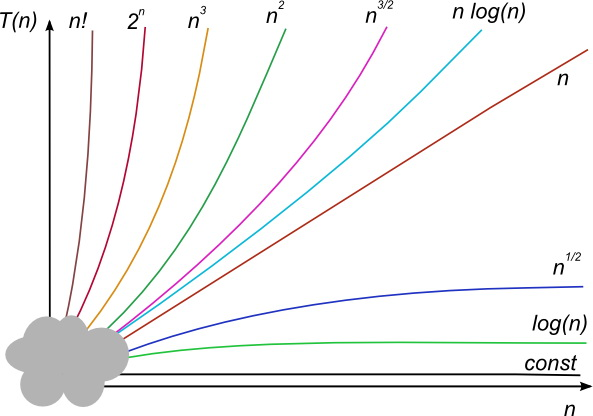 1.6. ábra. A gyakran előforduló nagyságrendek grafikonja
1.6. ábra. A gyakran előforduló nagyságrendek grafikonjaMegadunk néhány példát az algoritmusok aszimptotikus futási idejére.
Verem vagy sor bármely művelete | 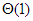 |
Logaritmikus (=bináris) keresés | 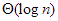 |
Prímszámteszt (n1/2-ig) | 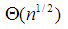 |
Lineáris keresés | 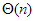 |
Kupacrendezés | 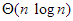 |
Shell rendezés | 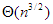 |
Buborékrendezés | 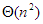 |
Mátrixszorzás | 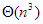 |
Hanoi tornyai | 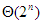 |
Utazó ügynök probléma | 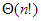 |
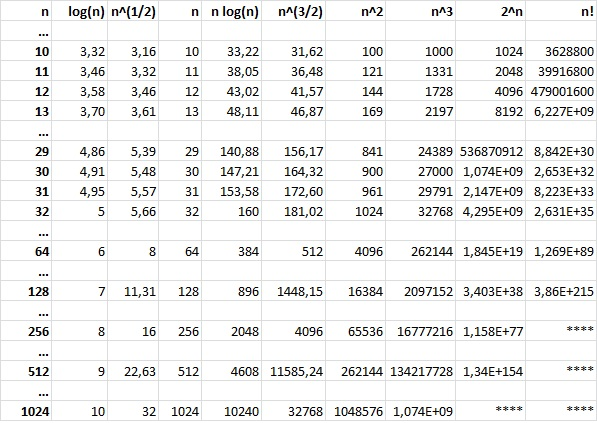
A műveletigények gyakran előforduló nagyságrendjeinek értékeit az 1.7. ábrán látható tartalmazza néhány jellegzetes n értékre, mindössze 1024-ig. Az n=12 nevezetes érték az n! függvény esetében. A 12! még egészként ábrázolható, a 13! már csak lebegőpontos számként, és egy n! műveletigényű probléma egzakt teljes körű megoldása általában az n=12 értékre még kivárható egy erős asztali gépen, de nagyobb értékekre már nem. Ezt a 108 nagyságrendű határt a 2n függvény 29-nél éri el, az n3-ös műveletigényű algoritmusok pedig 500 felett nem sokkal. Figyelemre méltó még az is, hogy az n2 és az nlog(n) értékek n=1024 esetén (ami a gyakorlatban csekély adatmennyiség) már két nagyságrendben térnek el. (Néhány olyan értéket, amely a Matlab programban túlcsordulást okozott, nem helyettesítettük kiszámolt értékekkel, hiszen ezeknek a nagyságrendeknek nincs valós értelmük; nem csak az algoritmusok világában, de a földi tér-idő mennyiségek szempontjából sem.)
Látszik, miért mondják az informatikusok, hogy legfeljebb az n3-ös algoritmusoknak vesszük hasznát a gyakorlatban. Az is nyilvánvaló, hogy nagyobb n-ekre miért érdemes nlog(n) műveletigényű rendezéseket használni az n2-es eljárásokkal szemben, illetve miért érdemes a gráfos algoritmusokat gyorsítani – például minimumválasztó kupac adatszerkezet alkalmazásával –, hiszen ott is ez a két utóbbi nagyságrend állítható egymással szembe.
 1.7. ábra. A gyakran előforduló nagyságrendek értékeinek táblázata
1.7. ábra. A gyakran előforduló nagyságrendek értékeinek táblázataA táblázat valós értékei jól érzékeltetik azt, hogy mennyire fontos az algoritmusok műveletigényével tisztában lenni, és azt a lehetőség szerint minél alacsonyabbra választani.
 |
 |
 |
A tananyag az ELTE - PPKE informatika tananyagfejlesztési projekt (TÁMOP-4.1.2.A/1-11/1-2011-0052) keretében valósult meg.
A tananyag elkészítéséhez az ELTESCORM keretrendszert használtuk.