A mintaillesztés feladata az, hogy egy szövegben egy szövegminta (szövegrészlet, string) előfordulását vagy előfordulásait megkeressük. A mintaillesztés elnevezés mellett találkozunk a stringkeresés elnevezéssel is.
A feladat általánosítható: valamely alaptípus feletti sorozatban keressük egy másik (általában jóval rövidebb) sorozat előfordulásait (például egy DNS láncban keresünk egy szakaszt).
A továbbiakban egyszerűsítjük a feladatot a minta első előfordulásának a megkeresésére, amelynek segítségével az összes előfordulás megkapható. (Keressük meg a minta első előfordulását, majd a hátralévő szövegben ismét keressük az első előfordulást stb.)
Vezessük be a fejezet egészére az alábbi jelöléseket:
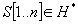 , azaz egy n hosszú H feletti véges sorozat.
, azaz egy n hosszú H feletti véges sorozat.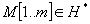 , egy m hosszú szintén a H feletti véges sorozat.
, egy m hosszú szintén a H feletti véges sorozat.Továbbá, tegyük fel, hogy S-en és M-en megengedett művelet az indexelés, azaz hivatkozhatunk a szöveg vagy a minta egy i-edik elemére S[i] (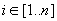 ), M[i] (
), M[i] (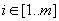 ).
).
A tárgyalt algoritmusok némelyike lényeges módosítás nélkül átírható szekvenciális fájlokra is (ahol az indexelés nem megengedett), míg a más tárgyalt algoritmusok csak puffer használatával alkalmazhatók a csak szekvenciálisan olvasható hosszabb szövegekre.
Bevezetjük a minta előfordulásának fogalmát, több szóhasználatot is megemlítve. Legyen 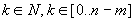 . Azt mondjuk, hogy
. Azt mondjuk, hogy
ha S[k+1..k+m]=M[1..m], azaz 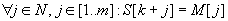 .
.
Továbbá, az M mintának a (k+1)-edik pozíción való illeszkedése az M első előfordulása az S szövegben, ha 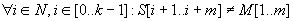 .
.
Legyen például a szövegünk S="ABBABCAB", és a keresett minta pedig M="ABC". A fenti definíció szerint az M minta a 4-edik pozíción, k=3 eltolással illeszkedik az S szövegre, ahogyan ez a 31.1. ábrán is látható.
 fej31_08_full.png31.1. ábra. Az M minta illeszkedése
fej31_08_full.png31.1. ábra. Az M minta illeszkedéseTekintsük megengedett műveletnek az azonos méretű sorozatok egyenlőségének a vizsgálatát, azaz esetünkben az S[k+1..k+m]=M[1..m] vizsgálatot.
Ekkor az a feladat, hogy keressük meg az első olyan k pozíciót (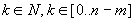 ), amelyre igazat ad a fenti vizsgálat. Ezt megtehetjük egy lineáris kereséssel.
), amelyre igazat ad a fenti vizsgálat. Ezt megtehetjük egy lineáris kereséssel.
A fejezett további részeiben is használt paraméterek jelentése legyen: 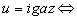
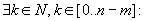 M a (k+1)-edik pozíción illeszkedik S-re, továbbá u=igaz esetén k visszatérési értéke az első érvényes eltolás. A lineáris keresésre épülő elvi megoldást, összhangban a most bevezetett paraméterekkel, a 31.2. ábrán láthatjuk.
M a (k+1)-edik pozíción illeszkedik S-re, továbbá u=igaz esetén k visszatérési értéke az első érvényes eltolás. A lineáris keresésre épülő elvi megoldást, összhangban a most bevezetett paraméterekkel, a 31.2. ábrán láthatjuk.
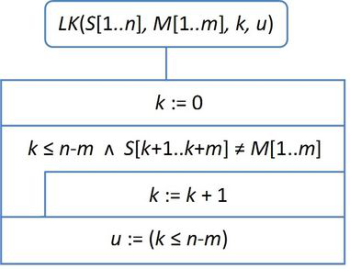 fej31_12_full.png31.2. ábra. Mintaillesztés lineáris kereséssel
fej31_12_full.png31.2. ábra. Mintaillesztés lineáris keresésselA stringkeresési feladat naiv megoldást egyszerű mintaillesztésnek fogjuk nevezni. Ehhez a nyers erő (brute force) algoritmushoz könnyen eljuthatunk a már tanult programozási tételekre való visszavezetéssel.
Folytassuk az előző részben elkezdett, lineáris keresésre épülő gondolatot. A vázolt megoldásban megengedett műveletnek tekintettük az S[k+1..k+m]=M[1..m] vizsgálatot. Ennek a kifejezésnek az eredményét megkaphatjuk karakterenkénti összehasonlítással is, amelynek során a minta minden karakterét összehasonlítjuk a szövegdarab megfelelő karakterével; és ha az összes vizsgált karakter egyezik, akkor a kifejezés értéke legyen igaz, különben hamis.
Az S[k+1..k+m]=M[1..m] vizsgálat előbb említett megvalósítása javítható, ha visszavezetjük lineáris keresésre, amelynek során keressük az első olyan 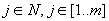 pozíciót, amelyre
pozíciót, amelyre 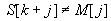 .
.
Amennyiben nem találunk ilyen j pozíciót, azaz 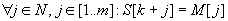 , akkor az M illeszkedik S-re k eltolással, tehát S[k+1..k+m]=M[1..m] vizsgálat eredménye legyen igaz, különben pedig hamis. Ezt a megoldást nevezzük az egyszerű mintaillesztés algoritmusának, amely nem más, mint egy lineáris keresésbe ágyazott lineáris keresés.
, akkor az M illeszkedik S-re k eltolással, tehát S[k+1..k+m]=M[1..m] vizsgálat eredménye legyen igaz, különben pedig hamis. Ezt a megoldást nevezzük az egyszerű mintaillesztés algoritmusának, amely nem más, mint egy lineáris keresésbe ágyazott lineáris keresés.
Az algoritmust szemléletesen úgy lehet elképzelni, mintha a mintát tartalmazó "sablont" tolnánk végig a szövegen, és balról jobbra ellenőrizzük, hogy a minta karakterei egyeznek-e a "lefedett" szöveg karaktereivel. Amennyiben nem egyező karakterpárt találunk, a mintát egy pozícióval jobbra "toljuk" a szövegen, és újra elkezdjük a minta elejéről az összehasonlítást. Az így kapott eljárás algoritmusát a 31.3. ábra tartalmazza.
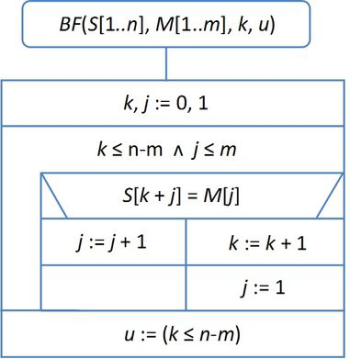 fej31_16_full.png31.3. ábra. Az egyszerű mintaillesztés algoritmusa
fej31_16_full.png31.3. ábra. Az egyszerű mintaillesztés algoritmusaNézzük meg egy példán az algoritmus működését. A 31.4. ábra első sorában szerepel a szöveg, alatta a minta a megfelelő eltolásokkal. A mintán ritka pontozású háttérrel jelöltük, azokat a karaktereket, amelyeknél az összehasonlítás igaz értéket adott, és sűrű mintázatú háttérrel, ahol az illeszkedés elromlott.
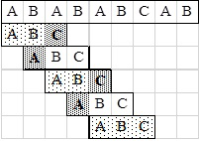 fej31_17_full.png31.4. ábra. Az egyszerű mintaillesztés működése
fej31_17_full.png31.4. ábra. Az egyszerű mintaillesztés működéseElőször mintát a szöveg első pozíciójára illesztjük, majd a mintán balról jobbra haladva vizsgáljuk a karakterek egyezését a szöveg megfelelő karaktereivel. A minta első illetve második karaktere ('A' és 'B') megegyezik a szöveg első és második karakterével, azonban a minta harmadik karaktere ('C') nem azonos a szöveg harmadik karakterével, tehát a minta nem illeszkedik az első pozícióra. "Toljuk el" a mintát egyel, majd a minta elejétől kezdve balról jobbra haladva ismét vizsgáljuk a karakterek egyezését a lefedett szövegrész megfelelő karaktereivel. Már a minta első karakterénél ('A') elromlik az illeszkedés. Ismét "toljuk el" eggyel jobbra a mintát, és a már ismertetett módon vizsgáljuk az illeszkedést.
Tizenegy összehasonlítás után eljutunk a végeredményhez, amely szerint a minta az 5. pozíción illeszkedik először a szövegre.
Műveletigény szempontjából a legjobb eset, amikor a minta az első pozíción illeszkedik a szövegre, ekkor az összehasonlítások száma minden mintaillesztő algoritmusnál m lesz. Ezt az esetet joggal tekinthetjük érdektelennek, mivel nem ad az algoritmus sebességére vonatkozóan valósághű jellemzést. Továbbiakban a mintaillesztési algoritmusok vizsgálata során mindig feltesszük, hogy a minta nem fordul elő a szövegben, így az algoritmusnak fel kell dolgoznia a "teljes" szöveget.
A különböző algoritmusok hatékonysága abban fog különbözni, hogy ebben az esetben mennyire "gyorsan" tudnak "végig menni" a szövegen. Tegyük fel még azt is, hogy a minta hossza nagyságrendben kisebb vagy egyenlő, mint a szöveg hossza, azaz 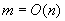 (a gyakorlatban a minta hossza jóval kisebb, mint a szöveg hossza).
(a gyakorlatban a minta hossza jóval kisebb, mint a szöveg hossza).
Ezek előre megadjuk az egyszerű mintaillesztés műveletigényét. A legjobb esetben a minta első karaktere egyáltalán nem szerepel a szövegben, így minden k eltolásnál már j=1 esetben mindig elromlik az illeszkedés. Tehát minden eltolásnál csak egy összehasonlítás történik, így az összehasonlítások száma megegyezik az eltolások számával, (n-m+1)-gyel. Tehát 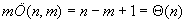 .
.
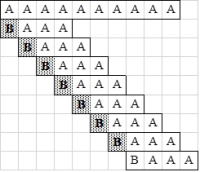 fej31_20_full.png31.5. ábra. Példa az egyszerű mintaillesztés legjobb esetére
fej31_20_full.png31.5. ábra. Példa az egyszerű mintaillesztés legjobb esetéreA legkedvezőtlenebb esethez akkor jutunk, ha minden eltolásánál csak a minta utolsó karakterénél romlik el az illeszkedés. Ekkor minden eltolásnál m összehasonlítást végzünk, így a műveletigény az eltolások számának m-szeresével jellemezhető. Tehát 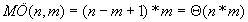 .
.
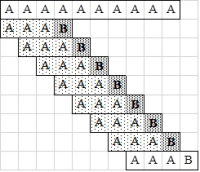 fej31_22_full.png31.6. ábra. Példa az egyszerű mintaillesztés legrosszabb esetére
fej31_22_full.png31.6. ábra. Példa az egyszerű mintaillesztés legrosszabb esetéreA gyakorlatban az általunk szövegnek nevezett sorozat nem egyszer igen nagyméretű is lehet, emiatt csak olyan szekvenciális formában áll rendelkezésünkre, amelyen az indexelés nem megengedett művelet. Hasznos lehet annak vizsgálata, hogy az ismertetett algoritmust mennyire egyszerű átírni szekvenciális sorozatokra, illetve fájlokra. Az egyszerű mintaillesztő algoritmus szekvenciális sorozatokra történő átírásánál kénytelenek vagyunk puffert használni, mivel a szövegben időnként vissza kell "ugrani" (akkor, ha az illeszkedés nem a minta első karakterénél romlik el).
 |
 |
 |
A tananyag az ELTE - PPKE informatika tananyagfejlesztési projekt (TÁMOP-4.1.2.A/1-11/1-2011-0052) keretében valósult meg.
A tananyag elkészítéséhez az ELTESCORM keretrendszert használtuk.