35. Mintaillesztés automatával

Ha ma tudni szeretnénk, hogy mi Zimbabwe fővárosa, mikor írta Petőfi az Anyám tyúkját, mi a szinusz függvény definíciója, akkor ma már nem állunk neki a lexikonok böngészésének, hanem az Internetet hívjuk segítségül. Valamelyik kereső programba beírjuk azt a tudásmorzsát, amelyet az adott kérdéskörből ismerünk. A program az Interneten lévő dokumentumok közül felsorolja mindazokat, melyek illeszkednek az előbbi tudáselemhez. Beütve például a Google-ba a „Zimbabwe” szót, felsorolásra kerülnek a Zimbabwéről szóló dokumentumok. Ezek között előkelő helyen ott lesz a Wikipedia Zimbabwét bemutató cikke, melyben aztán megtalálhatjuk a főváros nevét. A tudásmorzsa a legtöbbször – mint előbb is – valamilyen szó, a keresés számára egy minta, és azokat a dokumentumokat kapjuk vissza valamilyen sorrendben, melyekben ez a minta előfordul.

A szövegfeldolgozó rendszerek, például a Word is, kínálnak hasonló jellegű lehetőségeket. Ha ebben a jegyzetben meg szeretnénk keresni, mi a mintaillesztés fogalma, akkor a Word keresés funkciójánál begépeljük a „mintaillesztés” szót, beállítjuk az „összes” opciót. A keresés eredményként az jegyzet elejétől kezdve rendre villogva ráállhatunk a „mintaillesztés” szó előfordulásaira, melyek között ott lesz az is, amely a definíciót tartalmazza.

35.1. A mintaillesztési feladat

Az bevezetőben szereplő két példa a mintaillesztési feladat két lehetséges változatát mutatja be. Az első esetben a feladat az, hogy valamely szövegről eldöntsük, hogy benne van-e részszövegként az adott minta (ezek összességét kell azután felsorolni). A második esetben nem csak el kell döntenünk, hogy szerepel-e a szövegben az adott minta, hanem annak összes lehetséges előfordulását is meg kell keresnünk. Világos, hogy a második feladat megoldásával az első feladatot is megoldjuk, hiszen a minta első előfordulása után már jelezhetjük, hogy a minta megtalálható a szövegben.

Fogalmazzuk meg pontosan a feladatot. Ehhez szükségünk lesz néhány jelölésre, illetve fogalomra.

A fejezetben legyen X egy rögzített ábécé (véges, nem üres szimbólumhalmaz), X* az X elemeiből képzett véges sorozatok halmaza, míg X⁺a nem üreseké. Egy u∈X* szó, mint sorozat hosszára |u| jelölést fogjuk használni.

Az X* elemeit X ábécé feletti szavaknak, vagy X rögzítettsége esetén egyszerűen csak szavaknak hívjuk. Az üres szó jele ε.

Tetszőleges u∈X* és h0 esetén definiáljuk u szó h hosszú kezdőszeletét (végszeletét), mely h≤|u| esetén u első (utolsó) h jele, illetve az egész u, ha |u|<h. Az első esetben valódi kezdőszeletről (végszeletről) beszélünk. Jelölésük pre(u,h), illetve suf(u,h) (a nekik megfelelő angol szavak, prefix, illetve suffix rövidítésével).

(Megjegyezzük, hogy ez a terminológia kissé megtévesztő, hiszen a h hosszú kezdőszelet (végszelet) hossza csak h≤|u| esetében h hosszúságú szó, egyébként magának az u-nak a hosszával egyenlő.)

Rögzítsük most X* egy m=m₁m₂...m_|m| nem üres szavát, melyet mintának fogunk nevezni.

Azt mondjuk, hogy m illeszkedik az u∈X* szóhoz, ha u felírható az u=vmw alakban, ahol v és w X feletti szavak. Az m illeszkedik az u elejéhez (végéhez), ha illeszkedik hozzá és v = ε (w = ε).

Definíció: Az m minta illeszkedési függvénye, ill_m egy olyan ill_m:X*→ {0,1}* leképezés, melyben tetszőleges u∈X* mellett |ill_m(u)| = |m| +1. Továbbá, minden 0≤i≤|u| esetén: ill_m(u)_i+1= 1⇔az u szó i hosszú kezdőszeletének végéhez illeszkedik az m minta.

Definíció: A mintaillesztés feladata valamely m∈X* mintára az ill_milleszkedési függvény előállítása.

A feladatot egy olyan algoritmussal fogjuk megoldani, amely által megvalósított
λ:X*→ {0,1}* függvényre λ=ill_m.

Világos, hogy λ=ill_mpontosan akkor teljesül, ha minden v∈X* szóra teljesül, hogy λ(v)_|v|+1=1⇔v végére odailleszthető az m minta. (u kezdőszeleteit választjuk rendre v-nek). A megoldás helyességének belátásához a továbbiakban ezt a tulajdonságot fogjuk ellenőrizni.

A feladatot speciális algoritmussal, megjelölt állapotú, véges, determinisztikus automatával fogjuk megoldani. Később látni fogjuk, hogy ezt az automatát megvalósíthatjuk valamilyen szokásos, algoritmusokat leíró nyelven.

Vissza a tartalomjegyzékhez

35.2. Megjelölt állapotú véges determinisztikus automaták

A megjelölt állapotú véges, determinisztikus automata egy absztrakt matematikai gép, melynek sémája a következő 35.1. ábrán látható.

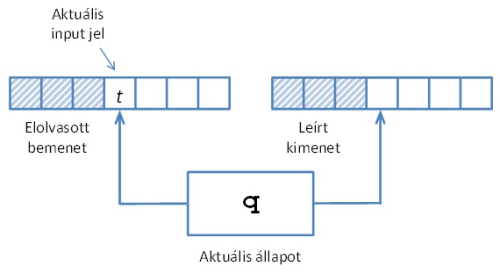A kép (nagyobb változata) külön ablakban is megtekinthető.fej35_549_full.png35.1. ábra. Megjelölt állapotú automata

A gép diszkrét időskálában működik. Elindul egy kezdeti állapotból és ütemenként elolvassa a bemeneti szalagján lévő jeleket. Egy ütem során aktuális állapota és az olvasott bemenő jel függvényében új állapotba megy át. Minden érintett állapot esetén (tehát a kiinduló állapotban is), kiad egy Y-beli, csak az állapottól függő kimeneti jelet. A működés eredménye a kimenetre írt, a bemeneti szónál eggyel hosszabb szó. A megjelölt állapotú véges, determinisztikus automatára adott informális leírást a következő módon formalizálhatjuk:

Definíció: Az A=<A,X,Y,δ,a₀,μ> hatost megjelölt állapotú véges, determinisztikus automatának nevezzük, ahol

• A: véges halmaz, az automata állapotainak halmaza,
• X: ábécé, az automata bemenő jeleinek halmaza,
• Y: ábécé, az automata kimenő jeleinek halmaza,
• δ:A×X → A alakú, mindenütt értelmezett leképezés, az állapot-átmeneti függvény,
• a₀:a₀∈A, az automata kezdőállapota,
• μ: A→ Y alakú, mindenütt értelmezett leképezés, a jelölő függvény.

Adjuk meg most az automata működési módját.

Egy u=u₁u₂...u_|u|∈X* bemenetre való működés leírásához először kiterjesztjük a δ állapot-átmeneti függvényt δ:A×X* → A alakú függvénnyé:

δ(a,u₁u₂...u_|u|)=a’⇔létezik olyan c₀c₁...c_|u|∈A⁺ sorozat, hogy c₀=a, c_n=a’ és minden i=0,1,n-1 esetén δ(c_i,u_i)=c_i+1.

A c₀c₁...c_n sorozat az u=u₁u₂...u_n bemenet feldolgozása során érintett állapotok sorozata (bele értve a kiinduló állapotot is).

Definiáljuk most a λ:A×X*→ Y* kimeneti függvényt a következő módon: λ(a,u₁u₂...u_|u|)=μ(c₀)μ(c₁)...μ(c_n), ahol c₀c₁...c_n az előbb definiált, a működés során érintett állapotsorozat

Világos, hogy tetszőlegesen rögzített a∈A, u∈X* és u=vw mellett igaz hogy |λ(a,u)|=|u|+1 és λ(a,u)=λ(a,v)suf(λ(δ(a,v),w),|w|).

Az A által megvalósított λ_A:X*→ Y* leképezés ezek után a következő: λ_A(u)=λ(a₀,u).

A véges automaták struktúráját és működését leírhatjuk a szokásos algoritmus leíró nyelvek valamelyikével is.

A δ átmeneti függvény értékeit tárolhatjuk egy Δ nevű, |A|×|X| méretű, A típusú mátrixban, míg μ-t egy nevű |A| méretű, Y típusú vektorban. Használunk még egy Aktáll nevű, állapot típusú változót, továbbá egy-egy X* típusú, illetve Y* típusú változót az Bemenet és Kimenet névvel.

Az Aktáll változót a₀-ra, míg Kimenet-et μ(a₀)-ra inicializálva rendre beolvassuk u elemeit az Bemenet-ről. A Δ mátrixból minden beolvasott jellel aktualizáljuk Aktáll-t (tehát végrehajtjuk az átmenetet), majd az M vektor alapján Aktáll (most már új) értékéből meghatározzuk a következő Y-beli kimenetet, amit a Kimenet végére írunk.

Amennyiben |A| nagy, akkor a Δ és M sok helyet foglalhat el. Ilyenkor a Δ-ban és M-ben való tárolást megpróbálhatjuk elkerülni úgy, hogy δ és λ érékét valamilyen eljárással, képlettel számítjuk ki. Ehhez persze az állapotokon valamilyen szabályszerűségeknek kell lenniük.

Vissza a tartalomjegyzékhez

35.3. Mintaillesztés megjelölt állapotú véges, determinisztikus automatákkal

Az m mintánkhoz olyan A megjelölt állapotú véges, determinisztikus automatát építünk, melyre λ_A=ill_m. Ehhez természetesen az Y={0,1} kimeneti ábécét fogjuk használni.

A konstrukció alapötlete, hogy A állapotaiban olyan információt tárolunk, mely alapján az addig beolvasott v∈X* bemenetről eldönthető, hogy a végéhez illeszkedik-e a minta. Ha igen, 1 választ adunk, egyébként 0-t.

Azt, hogy az előbb említett információ az automata minden ütemének végén ott van az állapotkomponensben, invariáns tulajdonságnak, vagy egyszerűen invariánsnak fogjuk nevezni.

Világos, hogy elegendő, ha az invariánsban szereplő információ nem a teljes v-től, csak annak |m| hosszú végszeletétől, suf(v,|m|)-től függ (hogy előtte mi volt v-ben, az nem befolyásolja m-nek a v végére való illeszkedését). Az is világos, hogy az invariánsnak teljesülnie kell az automata kezdőállapotára, továbbá az is, hogy az átmeneti-függvénynek olyannak kell lennie, hogy az x bemenet az invariáns tulajdonságot a w=suf(v,|m|) végszeletről átörökítse suf(wx,|m|)-re.

A legtermészetesebb ötlet az, hogy a tárolt információ legyen maga az |m| hosszú végszelet, hiszen így a vele való összehasonlítással |m| illeszkedése könnyen megállapítható. Később látni fogjuk, hogy ennél egyszerűbb struktúrájú információ is megfelel céljainknak.

Vissza a tartalomjegyzékhez

35.4. A „nyers erő” automata

A nyers erő automatában magukat a lehetséges |m| hosszú végszeleteket tárolja.

A nyers-erő automata ennek megfelelően a következő:

A^nyers=<{a_w;w∈X^≤|m|},X,{0,1},δ,a_∈,μ>

δ(a_w,x)=a_suf(wx,|m|),

μ(a_w)=1⇔w=m.

Az invariáns tulajdonság A^nyers-ben, hogy állapotaiban az addig elolvasott szó |m| hosszú végszeleteit (X^{≤ |m|}elemei) jegyzi meg. A kezdőállapotra, a_∈-ra ez nyilván, hiszen még nem olvastunk semmit. Az átmeneti függvény δ(a_w,x)=a_suf(wx,|m|)definíciója ezt az invariánst nyilván megőrzi. A v-re adott λ_A^nyers(v) kimenet utolsó, |v|+1-edik jele μ definíciója alapján pontosan akkor 1, ha v végéhez illeszkedik az m minta. Így λ_A^nyers=ill_m.

Az A^nyers automata megvalósításában Aktáll karakterlánc, melyet maximum |m| méretű sorként kezelünk. Az állapotváltás az olvasott szimbólumnak a sorba való berakásával történik. Annak ellenőrzéséhez, hogy Aktáll tartalma m (vagyis 1 vagy 0 kimenetet tartozik-e hozzá) a sort körbe kell pakolni. A körbepakolás ideje nyilván arányos |m|-el, ezért az egész szimuláció műveleti igénye arányos |u||m|-el.

Ahogy már utaltunk rá, nem feltétlenül szükséges az invariánsban a bemenet |m| hosszú végszeletét, mint sorozatot tárolni, Más reprezentáció, esetleg kevesebb tartalom is elég lehet az m-el való illeszkedés ellenőrzéséhez. Erre példák az alább ismertetett Rabin-Karp, Dömölky és Knuth-Morris-Pratt automaták.

Vissza a tartalomjegyzékhez

35.5. A Rabin-Karp automata

A Rabin-Karp automata alapötlete az, hogy X^≤|m|elemeit nemnegatív egész számokból álló párokkal kódoljuk és a nyers erő automata struktúráját és működését ezeknek a számpároknak a segítségével szimuláljuk. (Ebben az alfejezetben szám alatt mindig nemnegatív egész számot fogunk érteni.)

A számpárokkal való kódolás értelme az automata megvalósításánál jelentkezik, mert ekkor az Aktáll változó értéke nem karakterlánc lesz, hanem az őt kódoló számpár, melynek az elemein végzett műveletek gyorsan, konstans (|m|-től nem függő) idő alatt megvalósíthatók. (Ez persze csak akkor igaz, ha az adott szám befér programozási nyelvünk nemnegatív egész típusának értéktartományba. Erről később meg szót ejtünk.)

Először foglakozzunk a kódolással. Tekintsük X jeleit számjegyeknek, és vezessük be egy v∈X^* szó esetén a v jelölést a v, mint d-áris szám értékére (az üres szónak 0-t feletetve meg). A w∈X^{≤ |m|}alakú szavakat kölcsönösen egyértelműen kódolhatjuk a (|w|,w) alakú számpárokkal. (A |w| azért szerepel, hogy a kód egyértelműen visszakódolható legyen. Például a 0 kód minden olyan szó kódja lenne, mely nem tartalmaz a 0 jegytől különböző jegyet. Közülük a kódban tárolt hossz fog egyértelműen meghatározni egyet, nevezetesen az annyi 0-t tartalmazó szót, amennyi ez a letárolt hossz

Tekintsük most azt az állapot-átmeneti függvény definíciójánál jelentkező problémát, hogy ha ismerjük valamely w∈X^{≤ |m|}szó (e,f) kódját, akkor ebből hogyan határozhatjuk meg suf(wx,|m|) kódját.

Vizsgáljuk először az egyszerűbb, |w|=e<|m| esetet. Az x jel w mögé írása a d-áris számrendszerben d-vel való szorzásnak, majd x hozzáadásának felel meg. Ekkor tehát a kód (e+1,df+x).

Ha |w|=e=|m|, akkor először suf(w,|m|-1) kódját kell megkeresnünk, visszavezetve a dolgot az előbbi esetre. A d-áris számrendszer tulajdonságai miatt az első jegy leválasztása a d^|m|-1-el való maradékos osztással történhet, ahol az eredmény a maradék. Jelölje rem (f, d^|m|-1) ezt a maradékot. Ezzel a jelöléssel suf(w,|m|-1) kódja az (e-1,rem(f,d^|m|-1)). Az első eset képletét erre alkalmazva suf(wx,|m|) kódja (e,rem(f,d^|m|-1)+x) lesz. Jelöljük inc(e)-vel 0≤e<|m| esetén e+1-et, míg e=|m| esetén magát az e-t. Ezzel a jelöléssel suf(wx,|m|) kódja egységesen az (inc(e), rem(f,d^|m|-1 )+x) alakban írható.

Jelöljük Inf-fel a X^{≤ |m|}halmazon értelmezett w→ (|w|,w) kódolás értékeinek halmazát.
Inf:={(e,f);0≤e≤|m| és f legfeljebb |m| jegyű, d alapú szám}.

Az előbb bevezetett jelöléseket használva a Rabin-Karp automata a következő:

A^RK=<{a_e,f;(e,f)∈Inf},X,{0,1},δ,a_0,0,μ>

δ(a_e,f,x)=a_e’,f’,ahol(e’,f’)=(inc(e),rem(f,d^|m|-1)+x)

μ(a_e,f)=1⇔(e,f)=(|m|,m)

Az A^RK automata itt az A^nyers-nek ezzel a kölcsönösen egyértelmű kódolással való megvalósítása (így készítettük el), ezért λ_A^RK=λ_A^nyers,amiből λ_A^RK=ill_mmár következik.

Térjünk rá az implementáció műveleti idejére azon feltételezés mellett, hogy a kódban szereplő e és f ábrázolható a nyelvünk nemnegatív egész típusában. Ilyenkor Aktáll új értékének meghatározása az inc(e), rem(f,d^h-1)+x képletekkel konstans, |m|-től független, idő alatt történik, ezért a műveleti igény O(|u|).

Mit lehet tenni akkor, mikor az A^RK implementációja során az (e,f) kód második tagja, f nem fér el a nyelv nemnegatív egészeinek értéktartományába? (Hogy e se férjen el, az praktikusan úgysem fordulhat elő). Ilyenkor választunk egy olyan nagy p prímszámot, mely még ábrázolható a nyelvben egészként, és a kód második komponensében a számításokat modulo p végezzük. Ezzel kapcsolatosan két probléma lép fel.

Az első probléma az, hogy f≡m(modp) akkor is teljesülhet, ha f m. Ilyenkor nincs más, mint „visszalépve” |m| karaktert elvégezzük a nyers erő automatában látott vizsgálatot. Ehhez az állapotkomponensben tárolni kell (|w|,w) mellett a nyers erő automatában látott w-t is. Ezt a w egyenlő m plusz vizsgálatot szerencsére csak e=|m| és f≡m(modp) esetében, tehát csak ritkán kell elvégezni. (Ha az implementáció során az egész szöveg a rendelkezésünkre áll, akkor ennek a kiegészítő információnak a tárolására nincs is szükség, a visszalépést magában a szövegben is megtehetjük).

A második probléma, hogy hogyan történhet modulo p végzett számítás során rem(f,d^|m|-1) modulo p értékének meghatározása. rem(f,d^|m|-1)-et úgy is kiszámíthatjuk, hogy az f kódú w első jegyét beszorozzuk d^|m|-1-el, majd ezt a szorzatot vonjuk le f-ből. Ez a számítás már végezhető modulo p, de ismerni kell hozzá w első jegyét.

Ezt a nem modulo p számítás során f-ből visszakódolással ki tudnánk nyerni, de a modulo p értékéből már nem. Ezért most is szükséges az a |m| jellel való visszalépés. Ennek megvalósítása is a w-nek az állapot-komponensben való tárolásán alapszik. Amikor az őt tartalmazó sorból a berakás során kilép egy jel, az lesz az |m|-el való visszalépésnek megfelelő jel. Ha még nem lép ki semmi, akkor a kilépő jelnek a 0-t tekintjük.

Vissza a tartalomjegyzékhez

35.6. A Dömölky automata

A Dömölky automata alapötlete, hogy a lehetséges w ∈ X^≤|m|végszeletek helyett elegendő csak azt tárolni róluk, hogy végükre mely hosszakban illeszthető a minta eleje (illeszkedési hosszak). Az illeszkedési hosszak halmaza alapján egyértelműen eldönthetjük az m-hez való illeszkedést, hiszen ez akkor áll fenn, ha az illeszkedési hosszak között szerepel |m|.

Az illeszkedési hosszak halmazát leírhatjuk a karakterisztikus vektorukkal. Ez egy olyan |m| hosszúságú bitvektor, melynek valamely eleme akkor 1, ha a vektorbeli indexe illeszkedési hossz. Az ilyen vektorokat illeszkedési vektornak fogjuk nevezni és illvek(w)-vel jelöljük.

Az illeszkedési vektorok tekinthetők a w∈X^≤|m|szavak kódjaiként is, ahol persze ez a kód – a Rabin-Karp kóddal ellentétben – már nem kölcsönösen egyértelmű.

Hogyan lehet valamely w∈X^≤|m|szó előbb említett illeszkedési vektorából suf(wx,|m|) illeszkedési vektorát előállítani?

Mielőtt erre válaszolnánk, vezessünk be x∈X mellet x karvek(x)-el jelölt karakterisztikus vektorát. Ez is |m| hosszú bitvektor, melynek j-edik bitje pontosan akkor 1, ha a minta j-edik eleme x.

Rátérve az eredeti kérdésre világos, hogy suf(wx) illeszkedési bitvektorának első eleme pontosan akkor 1, ha x a minta első eleme. Az is világos továbbá, hogy az előbbi vektor j-edik komponense (1<j≤h) akkor 1, ha a minta j hosszan illeszthető wx végéhez. Ennek feltétele egyrészt, hogy az m minta (j-1) hosszan illeszkedjen az eredeti w-hez, továbbá hogy x a minta j-edik eleme legyen. Ezt a két feltételt együtt úgy fejezhetjük ki, hogy illvek(w)-t 1-gyel aritmetikailag jobbra léptetjük (az utolsó bit eltűnik, az első pedig 1), majd azt „és-eljük” karvek(x)-el (az azonos pozícióban levő bitekre alkalmazzuk a logikai „és” műveletet).

Definiáljuk most a Dömölky automatát a következő módon:

A^Döm=<{a_b;b∈{0,1}^|m|},X,{0,1},δ,a₀|m|,μ>,

δ(a_b,x)=a_b’,ahol b’=jobbrallép(b,1)∧karvek(x),

μ(a_b)=1⇔b utolsó komponense 1

Az invariáns tulajdonság, hogy a Dömölky automata állapotaiban az addig elolvasott szó |m| hosszú végszeleteinek (X^{≤ |m|}elemei) karakterisztikus vektorát jegyzi. A kezdőállapotban levő csupa 0 vektornak ezt kielégíti, mivel ekkor még nem olvastunk semmit, ezért egyezés sem lehet. Az átmeneti függvény definíciója korábbi okfejtésünk szerint ezt az invariánst megőrzi.

A v-re adott λ_A^Döm(v) kimenet utolsó, |v|+1-edik jele μ definíciója alapján pontosan akkor 1, ha v végéhez illeszkedik az m minta. Így λ_A^Döm=ill_m.

A megvalósítás során feltételezzük, hogy az aritmetikai jobbra léptetést tetszőleges hosszú bitsorozaton konstans idő alatt, nagyon gyorsan tudjuk elvégezni, s hogy hasonló igaz
az „és-elésre” és az utolsó bit kiolvasására is. Így a δ és μ számítása gyorsan, |m|-től független idő alatt történhet.

Emiatt a műveletigény most is O(|u|), de a Rabin-Karp automatához képest kisebb konstanssal. A karvek(x) vektorokat általában előre elkészítjük (prekondicionálás), amely folyamat |X||m| kiegészítő időt és térhelyet igényel.

Vissza a tartalomjegyzékhez

35.7. A Knuth-Morris-Pratt automata

A Knuth-Morris-Pratt automata alapötlete, hogy a Dömölky automatában szereplő bitvektor helyett elegendő azt tárolni, hogy abban melyik pozíción van benne az utolsó 1-es. Feltéve, hogy ez a pozíció a j-edik, akkor ebből m alapján a teljes bitvektor rekonstruálható, hiszen értéke pontosan ott 1, ahány jelre m a pre(m,j) végéhez illeszthető. A Dömölky automatára való utalás nélkül ez úgy fogalmazható meg, hogy Knuth-Morris-Pratt automata állapotában a mintának a bemenő szó végéhez való leghosszabb illeszkedésének hosszát tárolja.

Hogyan lehet egy w∈X^≤|m|szó előbb említett maximális illeszkedési hosszából suf(wx,|m|) hasonló maximális illeszkedési hosszát előállítani?

Legyen j a w-hez való illeszkedés maximális hossza. A wx-hez való illeszkedés maximális hosszát úgy kapjuk meg, hogy m₁m₂...m_jx végére illesztjük maximális hosszan m-et (w korábbi elemeit nem kell figyelembe venni, mert ha a teljes w alapján hosszabb illeszkedést kaphatnánk, akkor j nem lenne maximális illeszkedési hossz w-hez).

Definiáljuk most a Knuth-Morris-Pratt automatát a következő módon:

A^KMP=<{a_j;0≤j≤|m|},X,{0,1},δ,a₀,μ>,

δ(j,x)=a_j’, ahol j’=Max{k;suf(m₁m₂...m_j,k)=pre(m,k)}

μ(a_j)=1⇔j=|m|

Az invariáns tulajdonság, hogy a Knuth-Morris-Pratt automata állapotaiban az addig elolvasott szó |m| hosszú végszeleteinek (X^≤|m|elemei) maximális illeszkedési hosszát jegyzi meg. A kezdőállapotban nyilván 0-nak kell lennie, hiszen még nem olvastunk semmit, ezért egyezés sem lehet. Az átmeneti függvény definíciója korábbiak szerint ezt az invariánst megőrzi.

Az A ^KMP automata az A ^Döm-nek kölcsönösen egyértelmű kódolással való megvalósítása (így készítettük el), ezért λ_A^KMP=λ_A^Döm, amiből λ_A^KMP=ill_mmár következik.

A megvalósítás során Aktáll-ban csak a 0,1,...,|m| értékeket kell tárolni, ami log₂(|m|) biten történhet. A δ függvényt itt is, ahogy azt a Rabin-Karp és Dömölky automatáknál is tettük, képlettel számoljuk. Nagy eltérés viszont, hogy δ definíciójában szereplő
j’=Max{k;suf(m₁m₂...m_j,k)=pre(m,k)} számítás direkt elvégzéséhez sok, |m|²-el arányos idő kell, emiatt a műveleti igény O(|m|²|u|) lenne.

Ezen segíthetünk úgy, hogy visszajátsszuk a számítást a Dömölky automatában látottakra. Ez utóbbihoz is szükséges O(|X||m|) idő, hiszen a maximális illeszkedésből az illeszkedési vektort elő kell állítani, illetve viszont. Így számolva a műveleti idő O(|m||X||u|).

Megtehetjük, hogy az átmenetek ütemenkénti számítása helyett előre kiszámítjuk a δ függvény összes értékét, amelyeket letárolunk a már említett Δ átmenet-mátrixba. A mátrix alapján az átmenet gyorsan végrehajtható, csak a mátrix megfelelő indexű elemét kell (konstans időben) elővenni. A műveleti idő ebben az esetben O(|u|) lesz, kicsi konstanssal. Ennek ára viszont, hogy prekondicionálásként szükség van a Δ mátrix számára (|m|+1)|X| darab log₂(|m|) bitnyi tárhelyre és összesen O(|X||m|²) időre.

Megjegyezzük, hogy ha csak az állapotok számát tekintjük, akkor a Knuth-Morris-Pratt automata optimális. Nincs |m|+1-nél határozottan kevesebb állapotot tartalmazó automata, amely a mintaillesztést megoldására terveztek. Ennek meggondolására tegyük fel, hogy volna ilyen. Vizsgáljuk meg az m bemenet mellett ennek az automatának a működését. Feltételezésünk szerint ebben az automatában δ(a₀,m₁m₂...m_|m|) 1-el van megjelölve. Ha c₀c₁...c_|m|∈A⁺ az érintett állapotok sorozata, akkor az előbbiek miatt c₀=a₀ és c_|m| megjelölése 1. A skatulya elv miatt közöttük van kettő, melyek egyformák (hiszen legfeljebb |m| különböző állapotunk van). Legyenek 1≤i<j≤|m| ezeknek az indexei. Az m₁...m_im_j...m_|m|szóhoz ekkor a c_0...c_ic_j+1...c_|m| sorozat tartozik, melyre c_|m| megjelölése 1. Ez azt jelenti, hogy m₁...m_im_j...m_|m| végéhez illeszkedne m, ami lehetetlen, hiszen m₁...m_im_j...m_|m|hossza határozottan kisebb, mint |m|.

Vissza a tartalomjegyzékhez

35.8. Összefoglalás

Összehasonlítva a négy automata felhasználási lehetőségeit a nyers erő automata az O(|m||u|) műveleti idő miatt csak kis mintahossz esetén működtethető gazdaságosan. A többi esetben a működési idő O(|u|), tehát nem függ |m|-től. Egy ütem számítási igénye a tárgyalás sorrendje szerint csökken. Ugyanakkor Dömölky automatánál szükség van |X||m| bitnyi tárhelyre és vele arányos időre a karvek vektorok kiszámításához. A prekondicionálásos Knuth-Morris-Pratt automata esetén viszont már jelentős többlet memóriát és futási időt igényel a prekondicionálás. Emiatt a Knuth-Morris-Pratt automatát akkor gazdaságos használni, ha ugyanazzal a mintával nagyon sok bemenő szóra kell a feladatot megoldani.

Vissza a tartalomjegyzékhez