Ebben a bevezető jellegű fejezetben arra a kérdésre próbálunk válaszolni, hogy az adattípusok, illetve adatszerkezetek milyen absztrakciós szinten jelennek meg az elméleti szintű megfontolások, a tervezés és a gyakorlati problémamegoldás során. Az itt következő meggondolások nem alkotnak egzakt elméletet, inkább csak egy ajánlható szemléletet tükröznek.
Az ismertetésben, amely felvázolja ezt a szemléletet, előzetesen hivatkoznunk kell olyan fogalmakra, amelyeket a következő fejezetekben vezetünk be részletesebben, a maguk helyén. Ebben a fejezetben mintegy előrehozott intuitív fogalmakra támaszkodunk. Úgy gondoljuk, hogy ezzel nem okozunk nehézséget az olvasóknak. A következő adattípusok szerepelnek példáinkban: tömb, verem, sor, listák, bináris fa és az elsőbbségi sor, valamint két speciális bináris fa: a kupac és bináris keresőfa. Ezekről az adatszerkezetekről a jegyzet későbbi külön fejezetei szólnak.
Egy elméletileg igényes programozó, aki specifikál, tervez és fejleszt, továbbá – mondjuk hiba esetén – a nyomkövetés eredményeként az adatszerkezet memóriabeli bitképét tanulmányozza, felfogásunk szerint az alábbi öt különböző absztrakciós szinten találkozik az adattípusokkal:
1. Absztrakt adattípus (ADT)
2. Absztrakt adatszerkezet (ADS)
3. Reprezentáció (ábrázolás)
4. Implementáció (fejlesztés, programnyelvi megvalósítás)
5. Fizikai (memória) szint
Ennek a tantárgynak a keretében az ismertetés az első három szinten marad, a programnyelvi implementáció és elemei adatszerkezetek (különféle számok, pointerek) bitképe nem része a tárgyalásnak.
A szóhasználatról előzetesen annyit, hogy az adatszerkezet bizonyos típusú adatelemek struktúrájára utal. Az adattípus kifejezés az adatszerkezet műveleteit is magában foglalja. Például, egy (láncolt) lista önmagában egy adatszerkezet, amely egyaránt megvalósíthat – többek között – vermet és sort. Azt a listát azonban, amely saját műveletekkel is rendelkezik, adattípusnak nevezzük. (Megjegyezzük, hogy a szóhasználat nem mindig konzekvens; olykor adatszerkezetet mondunk, de a műveleteket is hozzá értjük. Az adattípus és az adatszerkezet kifejezéseket gyakran szinonimaként használjuk, noha a típus elvileg többet fejez ki. Ez a szövegkörnyezet révén általában nem zavaró.)
Az ábrázolás, reprezentáció és a megvalósítás kifejezéseket nagyjából szinonimaként használjuk, közel azonos jelentéssel. Miután a nyelvi implementációs szint nem része az anyagnak, ez nem okoz félreértést.
Ez az adattípus leírásának legmagasabb absztrakciós szintje. Az adattípust úgy specifikáljuk ezen a szinten, hogy a szerkezetére (még) nem teszünk megfontolásokat. A leírásban kizárólag matematikai fogalmak használhatók. A specifikáció eredménye az absztrakt adattípus.
Az ADT szintű specifikáció lehet formális, mint a következő két példában, de lehet informális is: természetes magyar nyelven is elmondhatjuk, hogy mit várunk el például egy veremtől. A lényeg nem a leírás formalizáltsága, hanem az, hogy a specifikációban nem látjuk az adattípus belső struktúráját.
Mire jó az ADT szintű leírás?
A programozásról szóló könyvek és kurzusok azt tanácsolják, hogy ha egy feladatot szeretnénk megoldani, akkor előbb specifikáljuk az elvárásokat algoritmikus megfontolások nélkül, és csak utána keressük meg a megfelelő megoldó eljárásokat. Az ELTE-n a Programozás című tantárgy keretében egy – Dijkstra-tól eredő – specifikációs technikát használunk. Ebben megadjuk a feladat állapotterén (A), illetve paraméterterén (B) a bemenő adatokra fennálló előfeltételeket (Q), majd az utófeltétel (R) formájában megfogalmazzuk az eredményre vonatkozó elvárásainkat. Az elő-, és utófeltétel lényegében statikus logikai állításokat tartalmaz, így a specifikáció valóban nélkülözi az algoritmikus elemeket.
Az adatszerkezetek világában is adódhatnak hasonló természetű feladatok. Amikor például egy reprezentálási mód megválasztása a kérdés, célszerű, ha úgy tudjuk leírni az adattípussal kapcsolatos elvárásainkat, hogy nem teszünk megfontolásokat a szerkezetre nézve. Ilyen például az elsőbbségi (prioritásos) sor hatékony megvalósításának a problémája. Míg a legtöbben eleve tudják, hogy milyen a verem, vagy a sor adatszerkezet, addig kevesen hozzák magukkal köznapi ismereteik részeként az elsőbbségi sor reprezentálásáról szóló tudást. Mindenképpen hasznos tehát, ha szerkezeti összefüggések nélkül definiáljuk az elsőbbségi sor fogalmát.
Az ADT szintű leírás közvetíti az enkapszuláció gondolatát is. Ha valaki egy típust implementál, akkor az ezt tartalmazó modult várhatóan úgy írja meg, hogy magához az adatszerkezethez a felhasználó közvetlenül ne férhessen hozzá, hanem csak a műveleteken keresztül érhesse el azt. A másik oldalról, ugyanebben a szellemben, a program felhasználója is elfogadja, hogy közvetlenül nem nyúl bele egy adatszerkezetbe, hanem csak a műveletein keresztül használja és módosítja azt.
Alapvetően két leírási mód terjedt el: (1) az algebrai specifikáció, amely logikai axiómák megadásával definiálja az absztrakt adattípust, illetve (2) a funkcionális specifikáció, amely matematikai reprezentációval az elő-, utófeltételes módszerrel teszi ugyanezt.
Ebben a specifikációs módszerben először megadjuk az adattípus műveleteit, mint leképezéseket, az értelmezési tartományukra vonatkozó esetleges megszorításokkal együtt. Utána a műveletek egymásra hatásának értelmes összefüggéseit rögzítjük axiómák formájában. (Ez a leírási módszer bizonyára nem mondható mindenkihez közel állónak.)
A módszer alkalmazását a verem adattípus példáján mutatjuk be. A verem intuitív fogalma ismerős: olyan tároló struktúra, amelyből az utoljára betett elemet tudjuk kivenni. Ehhez nyilvánvalóan szerkezeti kép is társul, amelyről most tudatosan elfeledkezünk átmenetileg.
Először megadjuk a verem műveleteit, mint leképezéseket. Ezek közül talán csak az Üres művelet értelmezése lehet szokatlan: egyrészt létrehoz egy vermet, amely nem tartalmaz elemeket (lásd: deklaráció a programnyelvekben), másrészt az üres verem konstans neve is. Az Üres tehát egy konstans, ezért, mint leképezés nulla-argumentumú.
Az alábbi műveleteket vezetjük be.
Üres: → V | Üres verem konstans; az üres verem létrehozása |
Üres-e: V → L | A verem üres voltának lekérdezése |
Verembe: V × E → V | Elem betétele a verembe |
Veremből:V → V × E | Elem kivétele a veremből |
Felső:V → E | A felső elem lekérdezése |
Megadjuk a leképezések megszorításait. A Veremből és a Felső műveletek értelmezési tartományából ki kell vennünk az üres vermet, arra ugyanis ez a két művelet nem értelmezhető.
DVeremből=DFelső=V\{Üres}
Az algebrai specifikáció logikai axiómák megadásával valósul meg. Sorra vesszük a lehetséges művelet-párokat és mindkét sorrendjükről megnézzük, hogy értelmes állításhoz jutunk-e. Az alábbi axiómákat írjuk fel; magyarázatukat alább adjuk meg.
1. Üres-e (Üres) vagy v=Üres→Üres-e (v)
2. Üres-e (v)→v=Üres
3. ￢ Üres-e (Verembe (v, e))
4. Veremből (Verembe (v, e))=(v, e)
5. Verembe (Veremből (v))=v
6. Felső (Verembe (v, e))=e
7. Felső (v)=Veremből (v).2
Az 1. axióma azt fejezi ki, hogy az üres verem konstansra teljesül az üresség. Ezt változó használatával egyenlőségjelesen is megfogalmaztuk. A 2. axióma az üres verem egyértelműségét mondja ki. A 3. állítás szerint, ha a verembe beteszünk egy elemet, akkor az már nem üres. A 4-5. axiómapár mindkét sorrend esetén leírja a verembe történő elhelyezés és az elem kivétel egymásutánjának a hatását. Mindkét esetbe a kiinduló helyzetet kapjuk vissza. (Az utóbbiban a Verembe művelet argumentum-száma helyes, ugyanis a belső Veremből művelet eredménye egy (verem, elem) pár.) Az utolsó két állítás a felső elem és a vermet módosító két művelet kapcsolatát adja meg.
Egy ilyen axiómarendszertől először is azt várjuk, hogy helyes állításokat tartalmazzon. Természetes igény a teljesség is. Ez azt jelenti, hogy ne hiányozzon az állítások közül olyan, amely nélkül a verem meghatározása nem lenne teljes. Végül, a redundancia kérdése is felvethető: van-e olyan állítás a specifikációban, amely a többiből levezethető?
A funkcionális specifikáció módszerében először megadjuk az adattípus matematikai reprezentációját, amelyre azután az egyes műveletek elő-, utófeltételes specifikálása épül. A módszert a sor adattípusra mutatjuk be. Absztrakt szinten úgy tekinthetjük a sort, mint (elem,időpont) rendezett párok halmazát.
Az időpontok azt jelzik, hogy az egyes elemek mikor kerültek a sorba. Kikötjük, hogy az időpontok mind különbözők. Ezek után tudunk a legrégebben bekerült elemre hivatkozni.
A 2.1. ábrán szereplő absztrakt sornak öt eleme van és először (legrégebben) a 40-es érték került a sorba. Ez az absztrakt reprezentáció a veremre is megfelelő lenne! A verem esetén azt az elemet választjuk ki, amelyikhez a legnagyobb időpont tartozik, a sor esetében viszont éppen a legkisebb időponttal rendelkező érték az, amely aktuálisan kivételre kerül.
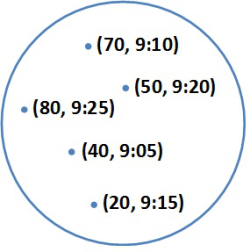fej2_01_full.png2.1. ábra. A sor (és a verem) absztrakciója, mint érték-időpont párok halmaza (ADT)Formálisan ez például a következőképpen írható le:
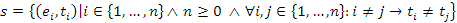
Ha a sor műveleteit szeretnék specifikálni, akkor azt most már külön-külön egyesével is megtehetjük, nem kell az egymásra való hatásuk axiómáiban gondolkodni. Definiáljuk például a Sorból műveletet. A programozás módszertanából ismert, említett elő-, utófeltételes specifikációval írjuk le formálisan, hogy ez a művelet a sorból az előkét betett elemet veszi ki, vagyis azt, amelyikhez a legkisebb időérték tartozik. (Ha az olvasónak nem lenne ismerős az alábbi jelölésrendszer, akkor elég, ha a módszer lényegét informális módon érti meg.)
A =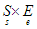 
B =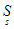 
Q = (s = s’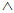 
s’ ≠ ∅)
R = (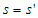
\
)
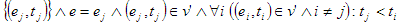A sor fenti absztrakt reprezentációja matematikai jellegű és nem tartalmaz semmiféle utalást a sor adattípus programnyelvi megvalósításának a módjára!
Az ADS szinten megmondjuk azt, hogy alapvetően (esetleg nem teljes részletességgel) milyen struktúrával rendelkezik a szóban forgó adattípus. Közelebbről ez azt jelenti, hogy megadjuk az adatelem közötti legfontosabb rákövetkezési kapcsolatokat, és ezt egy irányított gráf formájában le is rajzoljuk. Az absztrakt adatszerkezetet egy szerkezeti gráf és az ADT szinten bevezetett műveletek alkotják együttesen.
Ez az absztrakciós szint illeszkedik legjobban az ember kognitív sajátosságaihoz. Egy veremről nem az axiómák formájában őrzünk képet emlékezetünkben, hanem egy (feltehetően függőleges helyzetű) tömbszerű tároló jelenik meg előttünk. A verem kognitív sémája, amelyet gondolatainkban felidézünk, tehát nem gráf formájú, hanem inkább egy tömbre emlékeztet. A kétféle megjelenítés nyilvánvalóan megfelel egymásnak, ahogyan ezt a 2.2-es ábrán láthatjuk.
Általában ezen a szinten beszélünk és gondolkodunk az adatszerkezetekről. Az ADS szint felel meg legjobban a magyarázat, a megértés, a felidézés és az algoritmizálás, a tervezés és általában a kreatív problémamegoldás tevékenységének. Az egyes adatszerkezetek említésekor egy ilyen szintű ábra megjelenik meg gondolatainkban.
Az ADS szinten az adattípus legfontosabb szerkezeti összefüggéseit adjuk meg egy irányított gráffal. A gráf csúcspontjai adatelemeket azonosítanak, az irányított élek pedig a közöttük fennálló rákövetkezési relációt ábrázolják.
A 2.2. ábrán egy nagyon egyszerű gráf látható, amely egyetlen lineáris élsorozatot tartalmaz. Ez egyaránt ábrázolhat vermet, sort vagy listát. A szövegkörnyezet dönti el, hogy melyik adattípus absztrakt szerkezetét láthatjuk az ábrán. Ha veremről van szó, akkor említésre kerül, hogy a 40-es a felső elem. Sor esetén a 40-es az első, a 80-as pedig az utolsó elem. Ha egy lista ADS szintű ábráját látjuk, akkor viszont az aktuális elem fogalmát kell szóba hozni és meg kell mondani, hogy a melyik a lista aktuális eleme; lehet az például a 20-as.
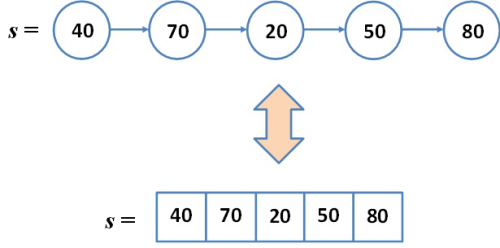fej2_08_full.png2.2. ábra. Lista (verem és sor) absztrakt szerkezeti ábrája (ADS)Tegyük fel, hogy most egy absztrakt sorral van dolgunk. Az ábrán látható kétféle megjelenítés (az egzakt és az informális) megfeleltethető egymásnak. Az utóbbi a sor tömbös ábrázolása felé mutat, míg az első a láncolt ábrázolás kiindulópontjának tekinthető.
Jellegzetes a bináris fa ábrája ezen a szinten, amellyel gyakran találkozhatunk. A 2.3. ábrán látható (gyökeres) bináris fa eredetileg irányított éleket tartalmaz, ám legtöbbször az irányítás lemarad az ábrákról. A rákövetkezéseket mutató nyilakat azonban odaértjük az élekre, szülő-gyerek irányban mindenképpen, de esetleg a fordított irányban is.
A bináris fák és általában a fák meghatározó szerepet játszanak az adatszerkezetek témakörében. Számos speciális fa adatstruktúrával találkozunk, amelyeket széles körben alkalmaznak az informatikában (ilyen például a kupac vagy a bináris keresőfa). Erről külön is szó lesz ennek a fejezetnek a végén. A bináris fákat általában láncoltan ábrázoljuk (erre mutat az ADS szintű ábra is, de speciális esetekben a tömbös ábrázolás adja a használható megoldást.
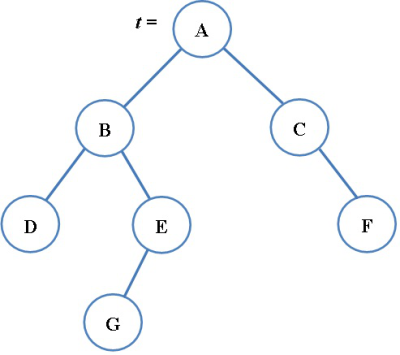fej2_09_full.png2.3. ábra. Bináris fa absztrakt szerkezeti ábrája (ADS)Az ADS szint előnyeit vegyük röviden sorra. Amint említettük, ez a szint illeszkedik legjobban az ember kognitív adottságaihoz. Ennek az lehet a magyarázata, hogy éppen kellően absztrakt: már megjelenik a struktúra, de még nem kell döntést hozni az ábrázolás módjáról. A szerkezeti összefüggések lényegét emeli ki, amelyeket majd a reprezentáció szintjén teszünk teljessé. Az ADS szint szemléletes, ami nem csak a struktúrára, hanem adattípushoz tartozó műveletek illusztrálására is vonatkozik.
Ezen a szinten arról hozunk döntést, hogy az ADS-szinten megjelenő gráf rákövetkezési relációit – kiegészítve azokat további szükséges szerkezeti összefüggésekkel – milyen módon ábrázoljuk. Két tiszta reprezentálási módot alkalmazunk. Ezek a következők: (1) az aritmetikai (tömbös) reprezentáció, illetve (2) a láncolt (pointeres) ábrázolás. Az így kapott ábrázolás már az implementációhoz közeli és a számítógépes megvalósítást modellezi.
Ha egy adattípust tömbösen ábrázolunk, akkor az adatszerkezet elemeit – alkalmas sorrendben – egy tömbben helyezzük el, a szerkezeti, rákövetkezési összefüggéseket pedig külön függvények formájában adjuk meg. Az adattípus részét képezik a tömb mellet bizonyos további attribútumok, amelyek általában indexekkel és más típusú (például logikai) változókkal fejezhetők ki.
A 2.4. ábrán egy verem tömbös ábrázolása látható.
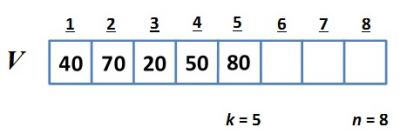fej2_10_full.png2.4. ábra. Verem tömbös reprezentálásaA reprezentációhoz tartozik a verem k mérete is. A verem elemei a tömb első és k-adik cellája között helyezkednek el. Az utoljára elhelyezett (a felső) elem éppen a k indexű tömbelem. Az üres vermet k=0 azonosítja, míg k=n esetén betelt a verem. Egy logikai hiba változót is a verem ábrázolásának a részévé tehetünk. A verem műveleteinek megírása is hozzá tartozik a tömbös reprezentáció elkészítéséhez. Ezt a veremről szóló fejezet tartalmazza.
A 2.5 ábrán egy teljes bináris fa és annak tömbös ábrázolása látható. A bináris és az általános fákat általában pointeresen reprezentálják. A teljes bináris fa esetében azonban hasznos lehet a tömbös ábrázolás is. A fa csúcsaiban található adatelemeket szintfolytonosan helyezzük el a tömbben.
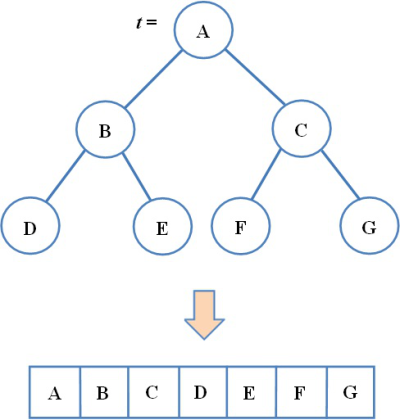fej2_11_full.png2.5. ábra. teljes bináris fa tömbös ábrázolásaA szülő–gyerek kapcsolatok szerencsére kezelhetők maradnak. Belátható ugyanis, hogy bármely c belső szülő csúcs és a bal(c) és jobb(c) gyerekcsúcsok tömbbeli indexei között fennáll a következő kapcsolat:
ind(bal(c))=2*ind(c)
ind(jobb(c))=2*ind(c)+1
Megfordítva, bármely nem-gyökér c gyerek csúcs és a szülő(c) csúcs indexei között érvényes az alábbi összefüggés:
ind(szülő(c))=⌊ ind(c) ⌋
A tömbös ábrázolás kulcsfontosságú a kupac adatszerkezetnél, ami ADS szinten nézve egy majdnem teljes balra tömörített bináris fa, reprezentálása azonban mindig tömbösen történik. Az absztrakciót előtérbe helyező szemléletünk számára fontos alátámasztást hordoz a kupac példája, amire visszatérünk ennek a fejezetnek a végén, illetve az elsőbbségi sorról és a kupacról szóló fejezetben.
Ehhez az ábrázoláshoz bevezetjük az absztrakt pointer (mutató) fogalmát. Ha p egy pointer típusú változó, akkor p→ jelöli az általa mutatott adatelemet. Ennek az adatelemnek a részeit, például az adat és mutató komponenseit a p→adat, illetve a p→mut hivatkozások választják ki. A sehová sem mutató pointer értéke NIL. A 2.6. ábrán látható láncolt struktúra részletben érvényesek például a következő egyenlőségek:
p→adat= 100; p→mut = q; p→mut→adat=200 stb.
fej2_12_full.png2.6. ábra. Láncolt ábrázolásMegegyezünk abban, hogy az absztrakt mutató típusos, azaz mindig valamilyen meghatározott típusú adatszerkezetre mutat. A láncolt ábrázolás algoritmusaiban tipikus helyzet, hogy egy új adatelemet kell létrehozni. Ezt a new(p) absztrakt utasítással tehetjük meg. Ennek hatására létrejön egy adott típusú, definiálatlan tartalmú adatelem, amelyre a p pointer változó mutat. Egy ilyen adatelem felszabadítása a dispose(p) absztrakt utasítással történik. Hatására az adatelem visszakerül a szabad helyek közé és p tartalma meghatározatlan lesz (általában még mindig az eldobott adatra mutat). A 2.7. ábra illusztrálja a létrehozás és a törlés műveletpárját.
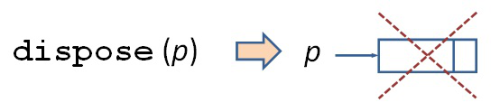fej2_14_full.png2.7. ábra. Láncolt adatelem létrehozása és törlésePéldaként tekintsük egy fejelemes lista láncolt ábrázolását, amelyet a 2.8. ábra mutat. A fejelemről röviden annyit, hogy az mindig szerepel egy ilyen típusú listában, még akkor is, ha a lista (logikai szinten) üres. A listának az az elemét, amelyre az akt pointer mutat, aktuálisnak nevezzük. A lista műveletei általában erre vonatkoznak. Ha akt=NIL, akkor éppen nincs kitüntetett aktuális elem a listában. A listákról szóló fejezetben több ábrázolási módot is bemutatunk és a lista műveleteit is bevezetjük.
fej2_15_full.png2.8. ábra. Fejelemes lista láncolt ábrázolásaKövetkező példánk legyen a 2.3. ábrán látható bináris fa reprezentálása pointeres módon. A láncolt ábrázolás egy részletét láthatjuk a 2.8. ábrán. A fa egyes csúcsainak megfelelő rekordok két pointer mezőt tartalmaznak. Ezek a bal és a jobb gyerekre mutató értékeket tárolják. A bináris fákról és a keresőfákról szóló fejezetekben olyan ábrázolási módot vezetünk be, amelyben a gyerek csúcsokból a szülőkre mutató pointerek is helyet kapnak.
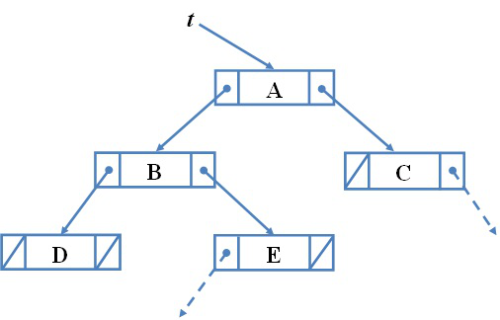fej2_16_full.png2.9. ábra Bináris fa láncolt ábrázolásaAz adatszerkezeteket algoritmusokban használjuk. Erre nagyszámú példát látunk a jegyzet egészében, de már az alapvető adatszerkezetekről szóló részben is. Az algoritmusok bármely szinten megjelenhetnek.
Az absztrakt adattípus (ADT) és az absztrakt adatszerkezet (ADS) szintjén csak a típusműveletek felhasználásával férünk hozzá az adatstruktúrához. Számos példát látunk majd az ADT szintű algoritmus leírásra. Például a helyes zárójelezés feldolgozásának algoritmusa műveleteivel használja a vermet (lásd: 4. fejezet).
Érdekes példát láthatunk a műveletek szintjén való gondolkodásra az elsőbbségi sornál (lásd: 8. fejezet). Ott szerepel az elsőbbségi sorral való rendezés algoritmusa. Az eljárás két nagyobb iteráció egymásutánja: először egyesével betesszük a rendezendő elemeket az elsőbbségi sorba, ezt követően pedig egymás után kivesszük és kiírjuk őket. A prioritásos sor – belső szerkezetétől független – működése garantálja azt, hogy az elemeket nagyság szerint csökkenő sorrendben kapjuk meg, egymás után. Ez egy magas absztrakciós szinten megfogalmazott rendező eljárás.
Ha a prioritásos sor három különböző reprezentációját tekintjük, akkor három ismert rendező algoritmushoz (pontosabban azokhoz igen közeli eljárásokhoz) jutunk; ezek a maximum kiválasztó, a beszúró és a kupacos rendezés.
Nincs olyan formai jegy, amely alapján egyértelműen el tudnánk dönteni, hogy egy absztrakt algoritmus-leírás ADT vagy ADS szintűnek mondható-e. Azt kellene ehhez megválaszolni, hogy az algoritmus megadásában kifejeződik-e annak ismerete, hogy milyen a benne szereplő adattípusok struktúrája. Ha például egy algoritmus bináris fát használ és hivatkozik egy csúcs bal vagy jobb gyerekére, szülőjére, akkor gyanítható, hogy a szerző látja maga előtt a bináris fa szerkezetét. Ám az alkalmazott függvények bevezethetők ADT szinten, a strukturális szemlélet nélkül is. szerencsére, ez az eldöntetlenség egyáltalán nem zavaró.
Az ADS szinten megfogalmazott eljárások jellegzetes példáját szolgáltatják a gráfalgoritmusok (lásd: VII. rész). A gráf absztrakt adatszerkezet megegyezik a gráf szemléletes matematikai fogalmával. A gráfalgoritmusok ilyen szinten történő leírása is szemléletes marad, ami részben elveszne, ha a mátrixos reprezentáció vagy a láncolt éllistás ábrázolást vennénk alapul.
Számos algoritmus leírását az ábrázolás szintjén adjuk meg. Az összes alapvető adatszerkezet műveleteit mind a tömbös, mind a láncolt reprezentációban megadjuk (lásd: II. rész). A későbbi anyagrészből merítve egy jellegzetes példát, a 11. fejezetben a bináris keresőfa műveleteinek algoritmusaival találkozhatunk a láncolt ábrázolás szintjén.
 |
 |
 |
A tananyag az ELTE - PPKE informatika tananyagfejlesztési projekt (TÁMOP-4.1.2.A/1-11/1-2011-0052) keretében valósult meg.
A tananyag elkészítéséhez az ELTESCORM keretrendszert használtuk.