A sor adatszerkezet is ismerős a mindennapokból, például a várakozási sornak számos előfordulásával van dolgunk, akár emberekről akár tárgyakról (pl. munkadarabokról) legyen szó. A sor adattípus informatikai alkalmazásai talán nem annyira sokszínűek, mint a verem felhasználásai, de a lényegesebbek között említhető a fák és a gráfok szélességi bejárása. Ezzel azonban majd a későbbi fejezetekben találkozunk.
Az E alaptípus feletti sorok S=S(E) halmazát azon sorok alkotják, amelyek véges sok E-beli elemet tartalmaznak. Ide soroljuk az üres sort is, amely nem tartalmaz elemet; ezt ennek ellenére, mint S(E)-beli sort, típusosnak tekintjük. A sor műveletei között szerepel az üres sor létrehozása (Üres), a sor üres állapotának a lekérdezése (Üres-e), adat betétele (Sorba), adat kivétele (Sorból) és annak az elemnek a lekérdezése (Első), amely kivételre következik.
Az utóbbi művelet neve (Első) utal arra, amit intuitív módon tudunk a sorról: az először, azaz legrégebben behelyezett elemet lehet kivenni, amely a sorban elől áll, vagyis az első elem. A sorból való kivétel és az első elem lekérdezésének műveletét ahhoz az előfeltételhez kötjük, hogy a sor nem üres. Absztrakt szinten úgy tekintünk a sorra, akár csak a veremre, mint amelynek befogadóképessége nincs korlátozva, így a Tele-e lekérdezést itt nem vezetjük be.
A sor adattípus absztrakt leírása során nem támaszkodhatunk szerkezeti összefüggésekre, ezért azok nélkül kell specifikálnunk ezt az adattípust is. A specifikációnak itt is ugyanazt a kétféle módját ismertetjük, amelyeket már láttunk a veremnél.
Megadjuk a sor műveleteit, mint leképezéseket. Az Üres művelet egyrészt létrehoz egy sort, amely nem tartalmaz elemeket (lásd: deklaráció a programnyelvekben), másrészt az üres sor konstans neve is. Az Üres egy nulla argumentumú leképezés. Az alábbi műveleteket vezetjük be.
Üres: → S | Üres sor konstans; az üres sor létrehozása |
Üres-e: S → L | A sor üres voltának lekérdezése |
Sorba: S × E → S | Elem betétele a sorba |
Sorból:S → S × E | Elem kivétele a sorból |
Első:S → E | A sor első elemének lekérdezése |
Ha a Sorból műveletet úgy definiálnánk, hogy a kivett elemet nem adja vissza, hanem eldobja be, akkor ez a törlésre szorítkozna. Ebben az esetben az első elem előzetes lekérdezésével ismerhetnék meg a sor elejéről törölt elem értékét.
A leképezések megszorításaihoz tartozik, hogy a Sorból és az Első műveletek nem értelmezhetők az üres sorra:
DSorból=DElső=S\{Üres}
Az algebrai specifikáció logikai axiómák megadását jelenti. A veremhez hasonlóan, itt is sorra vesszük a lehetséges művelet-párokat és mindkét sorrendjükről megnézzük, hogy értelmes állításhoz vezetnek-e. A következő axiómákat írjuk fel. az 1-es, illetve a 2-es index a pár első, illetve második komponensét jelöli: rendre egy sort, illetve egy elemet.
1. Üres-e(Üres) vagy s=Üres→Üres-e(s)
2. Üres-e(s)→s=Üres
3. ￢ Üres-e(Sorba(s,e))
4. Sorból(Sorba(Üres,e))=(Üres,e)
5. ￢ Üres-e(s) → Sorból(Sorba(s,e))2= Sorból(s)2
6. ￢ Üres-e(s) → Sorba(Sorból(s)1,e) = Sorból(Sorba(s,e))1
7. Első(s)=Sorból(s)1
Az 1. axióma azt fejezi ki, hogy az üres sor konstansra teljesül az üresség predikátuma. Ezt változó használatával, egyenlőségjelesen is megfogalmaztuk. A 2. axióma az üres sor egyértelműségéről szól. A 3. állítás szerint, ha a sorba beteszünk egy elemet, akkor az már nem üres. A 4. axiómával ki tudjuk venni a következő két állítás értelmezési tartományából azt az esetet, amikor az egymás után alkalmazott műveletpár üres sorból indul ki. Az 5-6. axiómapár a nem üres sorba történő elhelyezés és az elem kivétel egymásutánját írja le, mindkét irányból. Végül, az utolsó állítás az első elem és a sorból való kivétel kapcsolatát adja meg.
A helyesség, a teljesség és a redundancia kérdésében itt is érvényes az, amit a verem algebrai specifikációjánál mondtunk.
A funkcionális specifikáció módszerével, amely pusztán matematikai eszközöket használ, hasonló sor-fogalmat vezetünk be ahhoz, mint a verem esetében. Absztrakt szinten úgy tekinthetjük a sort, mint (elem,idő) rendezett párok halmazát. Az időpontok azt jelzik, hogy az egyes elemek mikor kerültek a sorba. Kikötjük, hogy az időpontok mind különbözők. Ezek után tudunk a legrégebben bekerült elemre hivatkozni. A 4.1. ábrán szereplő absztrakt sor megegyezik a verem ADT 4.1. ábráján láthatóval. A sornak öt eleme van és először (legrégebben) a 40-es érték került a sorba. Az absztrakt reprezentáció formálisan ugyanaz, vagyis megegyezik a veremre és a sorra, de a műveletek különbséget tesznek közöttük. A verem esetén azt az elemet választjuk ki, amelyikhez a legnagyobb időpont tartozik, a sor esetében viszont éppen a legkisebb időponttal rendelkező érték az, amely aktuálisan kivételre kerül.
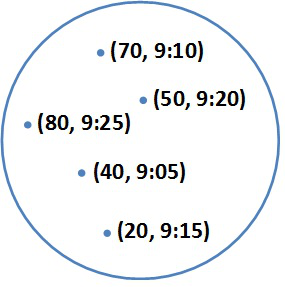5.1. ábra. A sor, mint érték-időpont párok halmaza (ADT)Formálisan ez például a következőképpen írható le:
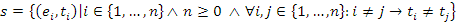
Ha a sor műveleteit szeretnék specifikálni, akkor azt most már külön-külön egyesével is megtehetjük, nem kell az egymásra való hatásuk axiómáiban gondolkodni. Definiáljuk például a Sorból műveletet. A programozás módszertanából ismert elő-, utófeltételes specifikációval írjuk le formálisan, hogy ez a művelet a sorból az előkét betett elemet veszi ki, vagyis azt, amelyikhez a legkisebb időérték tartozik. (Ha az olvasónak nem lenne ismerős az alábbi jelölésrendszer, akkor elég, ha a módszer lényegét informális módon érti meg.)
A =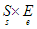 
B =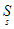 
Q = (s = s’ 
s’ ≠ ∅)
R = (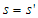
\
)
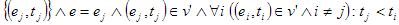A sor fenti absztrakt reprezentációja matematikai jellegű és nem tartalmaz semmiféle utalást a sor adattípus implementálásának a módjára.
A sor absztrakt szerkezete elemeinek lineáris struktúrájaként jelenik meg. Az 5.2. ábra úgy szemlélteti a sor ADS-t, mint egy speciális lineáris gráfot. Az ábrán az a megjelenési forma is látható, ahogyan a sor gondolatainkban jelentkezik, ahogyan a szakmai kommunikációban hivatkozunk rá. A két absztrakt szerkezet nyilvánvalóan megfeleltethető egymásnak.
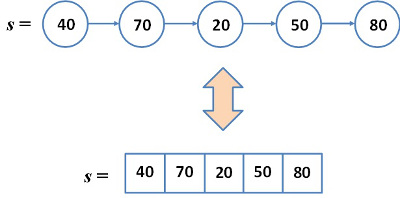5.2. ábra. A sor, mint rákövetkező elemek speciális gráfja (ADS)Az ADT szinten bevezetett műveletek az ADS szinten természetesen is változatlanul jelen vannak. Az a lényeget kifejező ábrázolási mód, amely ennek a szintnek a sajátja, jól használható arra, hogy a műveletek eredményét szemléletesen bemutassuk. Az 5.3. ábra a Sorba és a Sorból műveletek hatását illusztrálja.
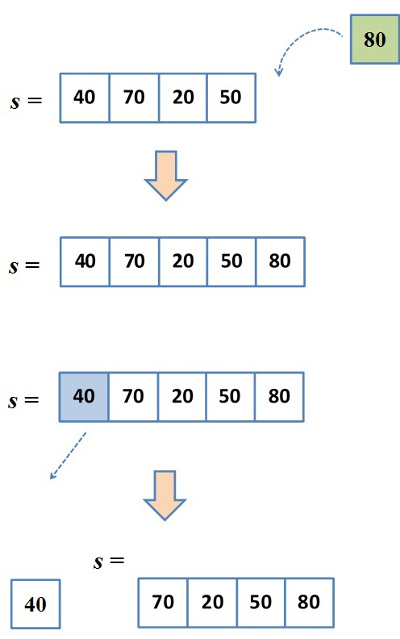5.3. ábra. Sor-műveletek szemléltetése (ADS)A sor adattípust egyaránt lehetséges tömbösen és láncoltan ábrázolni. Alább ismertetjük ezt a két reprezentálási módot.
Ha az 5.4. ábrára tekintünk, akkor egy sor három állapotát láthatjuk. Kezdetben a sor a tömb elején kezdődik, később azonban, ahogy kiveszünk belőle elemeket, a tömb belsejébe húzódik, majd elérve a tömb végét, a beszúrás ciklikusan folytatódik a tömb elején. Ennek megfelelően kétféle megoldás adódik a tömb eleje és vége jelzésére.
(1) Kézenfekvő az, hogy jelölje két index a sor elejét és végét. Ábráinkon e és j ez a két index. Ennek az ábrázolásnak az a hátránya, hogy az üres sor és a tele sor nem különböztethető meg a két index alapján. Ezen például úgy lehet segíteni, hogy a tömbben egy elemet kötelezően üresen hagyunk, vagyis a sor kapacitása egy elemmel kevesebb lesz, mint a tömb mérete.
(2) Egy másik lehetőség az, ha egy index jelzi a sor elejét és emellett megadjuk a sor hosszát. Ábráinkon e és h jelzi ezt a két értéket. Ekkor nem veszítünk elemet a tömbből.
A sor tömbös ábrázolásában az s[1..n] tömb mellett tehát (1) az első és utolsó elem indexét vagy (2) az első elem indexét és a sorhosszat használjuk, valamint a hiba logikai változót is a reprezentáció részének tekintjük. A sor s jelölése ezeket a komponenseket együttesen jelenti. Az 5.4. ábrán látható sor néhány állapotának tömbös ábrázolásban, a sor határainak mindkét fajta jelzése mellett.
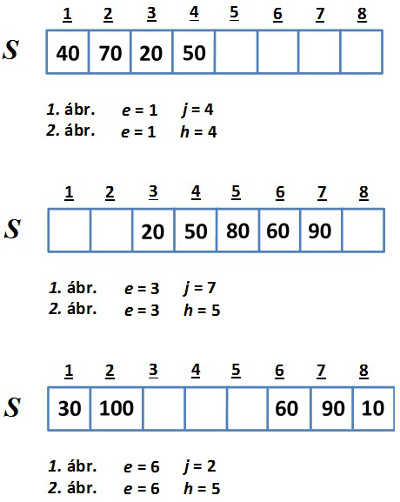5.4. ábra. Sor tömbös reprezentálásaAz ADS szintű ábra mellett a tömbös reprezentáció is alkalmas a műveletek hatásának bemutatására. Az 5.5.a és az 5.5.b ábra a Sorból és a Sorba műveletek eredményét illusztrálja szemléletes módon.
5.5.a. ábra. Sor-műveletek szemléltetése: Sorból (tömbös reprezentáció)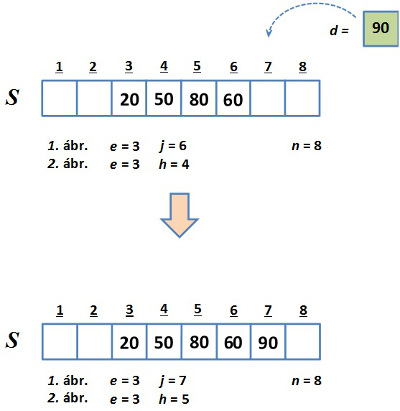
5.5.b. ábra. Sor-műveletek szemléltetése: Sorba (tömbös reprezentáció)Megadjuk a sor műveleteinek algoritmusait a tömbös reprezentációra. Ezen belül az első elem indexét és a sorhosszat használjuk a sor tömbbeli elhelyezkedésének azonosítására. Mivel az elemeket tároló tömb betelhet, ezért bevezetjük a Tele-e műveletet is, amely még ADT és ADS szinten nem szerepelt. Az üres vermet h=0 jelenti, míg h=n utal a tele veremre. A műveletek elvégzése után a hiba változó mindig értéket kap, sikeres művelet esetén hamisat, ellenkező esetben pedig a hibára utaló igaz értéket. A műveletek algoritmusai az 5.6. ábrán láthatók.
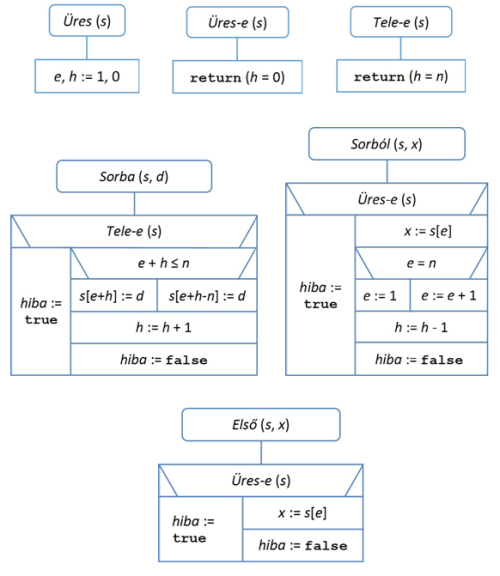fej5_28_full.png5.6. ábra. Sor műveletei tömbös reprezentáció eseténLátható, hogy a tömbös reprezentációban a sor bármely – op-pal jelölt – művelete, függetlenül a sor méretétől, konstans időben végrehajtható:
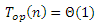
A sor láncolt reprezentációjában a s pointer típusú változó nem csak az adatstruktúrához biztosít hozzáférést, hanem egyben a sor első elemére is mutat. Ezért nem kell külön bevezetni egy első elem mutatót. Üres verem esetén s = NIL.
Az s pointer mellett bevezetjük az u pointert is, amely a sor utolsó elemére mutat. Ez azért hasznos, mert ekkor egy új elem befűzéséhez nem kell s-től indulni, hanem közvetlenül, konstans időben elvégezhető a Sorba művelet is.
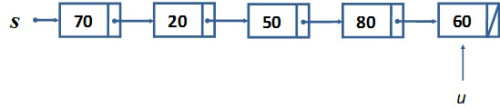fej5_19_full.png5.7. ábra. Sor láncolt ábrázolásaAz 5.7. ábrán látható sor megegyezik azzal, amelyet absztrakt szinten, illetve tömbösen vezettünk be. Az elemek sorrendje értelemszerűen olyan, hogy a verem utoljára betett felső eleme a lánc elején található. A kivétel ilyen módon mindig a lista első elemére vonatkozik, a beszúrás viszont az utolsó elem után fűzi be az új elemet. Ennek a két műveletnek a hatását mutatja be az 5.8.a és a 5.8.b ábra. A szemléletes képre gyakran szükség van a pointeres algoritmusok megírásakor.
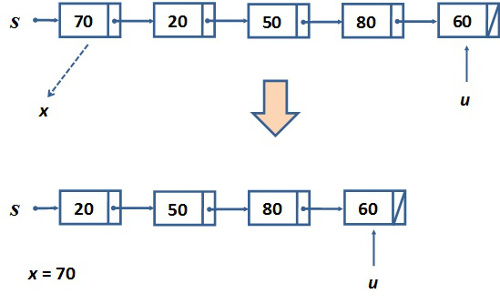fej5_20_full.png5.8.a. ábra. Sor-műveletek szemléltetése: Sorból (láncolt ábrázolás)
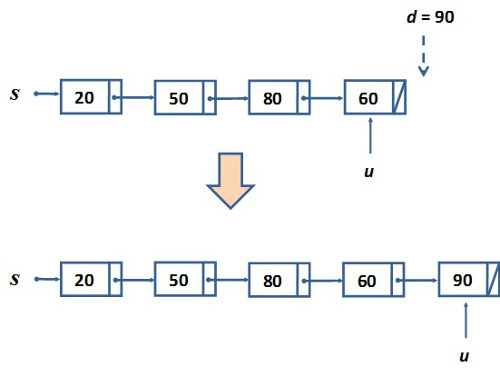fej5_21_full.png5.8.b. ábra. Sor-műveletek szemléltetése: Sorba (láncolt ábrázolás)Megadjuk a láncolt ábrázolású sor műveleteinek algoritmusait. A műveletek között ismét nem szerepel a betelt állapot lekérdezése, mivel ebben a reprezentációban nem számolunk a tárolókapacitás gyakorlati felső korlátjával.
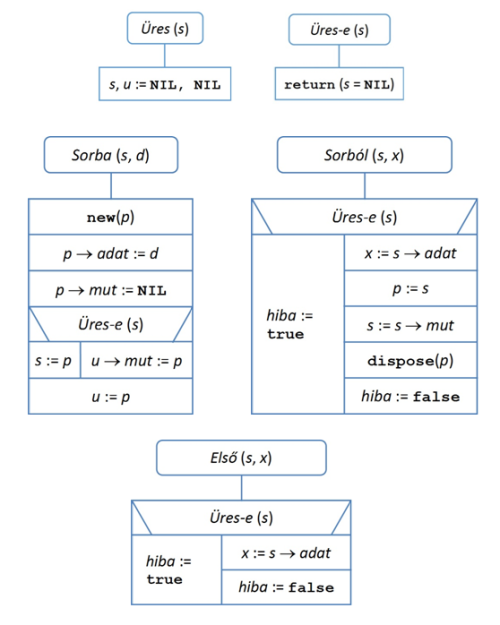fej5_30_full.png5.9. ábra. A sor műveletei láncolt ábrázolás eseténAz 5.9. ábrán látható algoritmusokban a sorba beszúrandó értéket adjuk meg a Sorba utasítás paramétereként, illetve a kiláncolt első elem értékét kapjuk meg a Sorból utasítás paraméterében. Ennek megfelelően a műveletek részeként a beszúrandó listaelemet létre kell hozni (new), illetve a kiláncolt listaelemet fel kell szabadítani (dispose).
Az utóbbi két műveletet úgy is meg lehet írni, hogy a Sorba egy kész listaelem pointerét kapja meg, míg a Sorból a kiláncolt listaelem mutatóját adja vissza. Ezzel a paraméter átadás-átvételi móddal majd a bináris keresőfa műveleteinél találkozunk.
A láncolt ábrázolás esetén is fennáll az, hogy a sor minden művelete – függetlenül a sor méretétől – konstans időben végrehajtható:
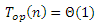
ahol op a sor műveleteinek bármelyikét jelentheti.
A sor adatszerkezet alkalmazásai közül kiemeljük a bináris fák szintfolytos és a gráfok szélességi bejárását. A sor adatszerkezet arra szolgál, hogy ezekben a struktúrákban a gyökértől, illetve a startcsúcstól induló és az élek mentén távolodó bejárást mintegy arra ortogonális irányúvá módosítsa. Ezzel a két algoritmussal későbbi fejezetekben találkozunk.
 |
 |
 |
A tananyag az ELTE - PPKE informatika tananyagfejlesztési projekt (TÁMOP-4.1.2.A/1-11/1-2011-0052) keretében valósult meg.
A tananyag elkészítéséhez az ELTESCORM keretrendszert használtuk.