A minimális költségű utak problémája olyan esetben is felmerül, amelyben a gráf élei negatív költségértékkel (súllyal) is rendelkezhetnek. Mindössze azt zárjuk ki, hogy a gráf negatív összköltségű kört tartalmazzon.
Gondoljunk egy olyan útvonal tervezési feladatra, amelyekben bizonyos útszakaszain bevételhez jutunk. A gráfos modellben egy él pozitív súlya azt jelenti, hogy azon a szakaszon a ráfordítás a nagyobb, míg a negatív költség arra utal, hogy ott a bevétel felülmúlja a kiadásainak. Ha egy negatív körön ismételten végighaladva, egyre növekedne a nyereségünk. Ezért a negatív körök kizárása a gyakorlat szempontjából is érthető feltétel.
Ebben a feladatban is egy kezdőcsúcsból a gráf összes csúcsához keressük a legkisebb költségű utat. A feladat megoldására a Bellman-Ford-algoritmust ismertetjük. Ez ugyanazt a közelítést alkalmazza az éleken, mint a Dijkstra-algoritmus, vagyis ha egy csúcshoz az addigi értéknél kisebb költségű utat talál az éppen vizsgált élen keresztül, akkor a csúcshoz ezt a javított értéket jegyzi be, valamint módosítja is az elérési útvonalat.
Az eljárás viszont nem követhet mohó stratégiát, szemben Dijkstra algoritmusával, ugyanis bármely már elért csúcs esetében előfordulhat az, hogy a még be nem járt csúcsok bevonásával – a negatív élkötségek folytán – javíthatunk a forrásból odavezető út addigi költségén.
Feladat. Adott egy G=(V,E) élsúlyozott, irányított vagy irányítás nélküli, negatív összköltségű kört nem tartalmazó véges gráf, továbbá egy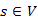 
forrás (kezdőcsúcs). Határozzuk meg minden v ∈ V csúcsra az s-ből v-be vezető legrövidebb utat, annak költségével együtt.
Vegyük szemügyre még egyszer a negatív kör jelenségét! A kezdőcsúcsból elérhető negatív összköltségű körön nem léteznének legkisebb költségű utak, mivel az illető körön tetszőlegesen sokszor végig menve az utak költsége mindig tovább csökkenthető lenne.
Irányítatlan gráf esetén, egy (u,v) negatív súlyú irányítatlan élen oda-vissza haladva az út költsége szintén korlátlanul csökkenthető lenne, azaz úgy viselkedne, mint egy negatív összköltségű kör. Tekintsük az irányítás nélküli élte tehát negatív összköltségű, két élből álló irányított körnek. Ez egybevág az ábrázolás szintjén megvalósított irányítatlan gráffal, ahol egy irányítatlan élt, egy oda-vissza irányított élpárral valósítunk meg. Tehát irányítatlan gráf esetén a megszorításunk az, hogy egyáltalán ne tartalmazzon negatív súlyú élt, mert az negatív irányított körnek tekinthető.
Minden csúcsra, ha létezik legrövidebb út, akkor létezik egyszerű legrövidebb út is, mivel a körök összköltsége nem negatív, így a kört elhagyva az út költsége nem nőhet. Egy n pontú gráfban, a legnagyobb élszámú egyszerű út hossza legfeljebb n - 1 lehet.
A Bellman-Ford-algoritmus a Dijkstra algoritmusnál megismert közelítés műveletét végzi, azaz egy csúcson át a szomszédba vezető él mentén vizsgálja, hogy az illető él része-e a legrövidebb útnak, javító él-e. Egy menetben az összes élre megvizsgálja, hogy javító él-e vagy sem. Összesen n - 1 menetet végez. (Az alfejezet végén visszatérünk az iterációk számára.)
Vizsgáljunk meg egy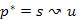 
legrövidebb utat. Minden menetben a 
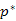minden élén végzünk közelítést. Legyen 
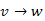él része 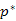-nak. Miután 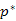v-ig tartó részútja 
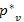ismertté válik, a következő menetben a 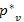is ismert lesz, mivel az (v,w) éllel is végzünk közelítést. Azonban az élek feldolgozásának (közelítésének) sorrendjére nem tettünk semmilyen megkötést, így csak azt tudjuk garantálni, hogy az első lépés után az 1 élszámú legrövidebb utak, a második lépés után a 2 élszámú legrövidebb utak, és így tovább, válnak ismerté. Mivel a leghosszabb egyszerű út n - 1 élszámú, ezért szükséges lehet az n - 1 menet.
A Bellman-Ford-algoritmus ADT szintű leírása a 25.1. ábrán látható.
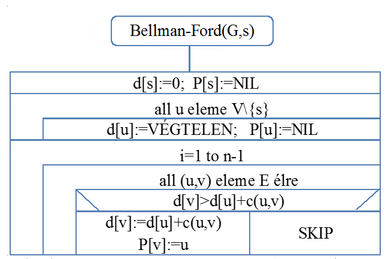25.1. ábra. A Bellman-Ford algoritmusÁllítás. Ha adott egy G=(V,E) élsúlyozott, irányított vagy irányítás nélküli, negatív összköltségű irányított kört nem tartalmazó véges gráf, továbbá egy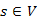 
forrás (kezdőcsúcs). Ekkor a Bellman-Ford algoritmus meghatározza 
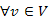csúcsra legrövidebb utat és annak hosszát.
Bizonyítás. Legyen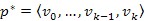 
egy s-ből u-ba vezető, egyszerű legrövidebb út, ahol 
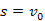és 
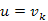. Teljes indukcióval belátjuk, hogy az i-dik menet után már ismert 
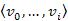legrövidebb részút, azaz 
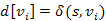és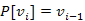 
, és ez már nem romlik el később sem.
Kezdetben az inicializáló lépés után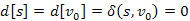 
. Ez fennmarad, különben létezne egy olyan s-ből elérhető u csúcs, amelyre 
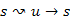és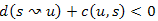 
, ami azt jelenti, hogy találtunk egy negatív kört.
A bizonyítás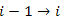 
általános lépésében tegyük fel, hogy ismert 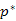-nak 
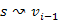részútja. Az i-dik menetben a 
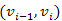éllel is végzünk közelítést (feljegyezzük 
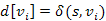és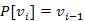 
), és ez csak akkor nem történik meg (
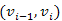nem javító él), ha 
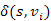már ismert, azaz a 
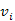-be vezető egyik legrövidebb utat már korábban megtaláltuk. Akésőbbiek során ez már nem változhat, mivel ha ez változna, az azt jelentené, hogy létezik a legrövidebb útnál rövidebb út, mivel 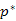is legrövidebb út és annak bármely részútja, így 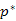-nak 
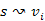részútja is legrövidebb út.
Mivel a legnagyobb élszámú, egyszerű, legrövidebb út élszáma is legfeljebb n-1, ezért a fenti indukciós állításból következik az algoritmus helyessége.
A Bellman-Ford algoritmussal gyakran abban a változatban lehet találkozni, amelyben még egy n-edik iteráció is szerepel, annak ellenőrzésére, hogy a gráf nem tartalmaz negatív kört. Ezt az jelzi, hogy a csúcsok költségértékek már nem változnak ebben az utolsó utáni menetben. (Negatív kör esetén a költségértékek tömbjében valahol csökkenést tapasztalnánk.)
Nézzük meg egy példán, ADS szinten az algoritmus működését. Tegyük fel, hogy az élek feldolgozási sorrendje a csúcsok címkéje szerint rendezett: (1,2), (1,3), ..., (5,3).
Az inicializáló lépés során beállítjuk a d[1..n] és P[1..n] tömb értékeit (25.2. ábra). A végtelen értéket most is '#' jellel jelöljük. Az első 7 él ((1,2)(1,3),....,(4,2)) közelítésénél nem történik változás, mivel végtelen értékek növelésénél szintén végtelent kapunk, ami nem javít. Csak két javító élt találunk. Most állíthatjuk, hogy minden csúcshoz megtaláltuk az s-ből hozzá vezető, minimális költségű, 1 élszámú utat.
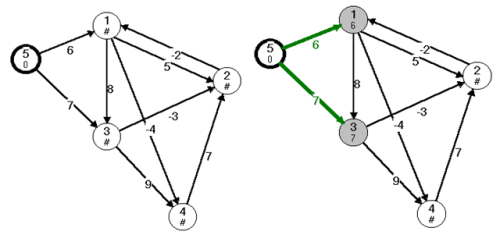fej25_s1_full.png25.2. ábra. Az algoritmus inicializáló és 1. lépéseA 2. lépésben a 2. és 4. csúcsokhoz találunk javító élt (25.3. ábra). Ezzel minden csúcshoz meghatároztuk a legkisebb költségű, 1 vagy 2 élszámú utat. Az utolsó lépésen látható az egyes csúcsokba vezető, 1 vagy 2 élszámú legrövidebb utakból kialakult fa. Ez a fa változhat, mivel lehet, hogy egy csúcsba el lehet jutni nagyobb élszámú olcsóbb úton is.
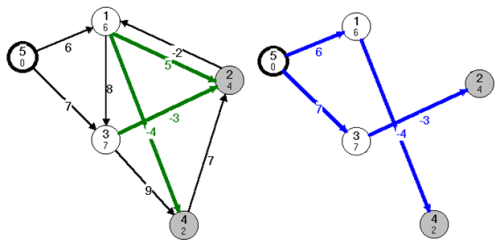fej25_s2_full.png25.3. ábra. Az algoritmus 2. lépése és a kialakult faA 3. lépésben az 1-be olcsóbb 3 élszámú utat találtunk (25.4. ábra). A fa változott mivel az 1-be már nem 1 élszámú, hanem 3 élszámú, de kisebb költségű úton juthatunk el a kezdőcsúcsból. A 4 megelőzője a korábban talált 1-es, csak most nem 2 élhosszú úttal, hanem 4 élhosszúval (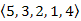
). Mivel az (1,4) élt korábban dolgoztuk fel, mint (2,1) élt, így a 4-es csúcsnál bejegyzett költség nem konzisztens a fával. (Az élek sorrendje hathat úgy, hogy az algoritmus az utak keresésében előresiet és megtalál egy hosszabb utat, mint ami az iterációk számából következne. Az ehhez számolt költség lehet helyes, és lehet helytelen, de ezt a megfelelő későbbi menetben korrigálja az eljárás.)
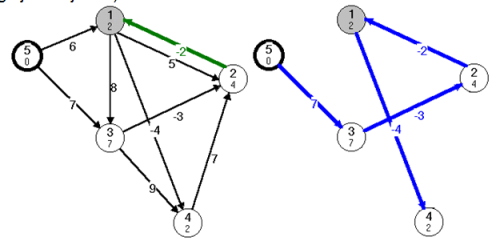fej25_s3_full.png25.4. ábra. Az algoritmus 3. lépése és a kialakult faA 4. lépésben (25.5. ábra) a fa már nem változik, csak 4-es csúcsnál bejegyzett költség veszi fel a helyes értéket.
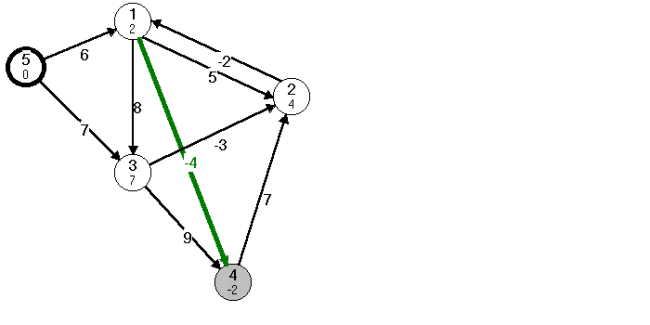fej25_08_full.png25.5. ábra. Az algoritmus 4. lépése és a kialakult faMivel n – 1 iterációt végzünk, és minden lépés során, minden élre végrehajtunk egy közelítést, ezért 
. Ez a műveletigény javítható a következő gyorsítással. (A buborék rendezésnél már láttunk hasonló gyorsítási lehetőséget.)
Állítás. Ha egy iteráció során nem következett be változás a közelítések során, akkor megállhatunk, az eljárás megtalálta az össze legkisebb költségű utat.
Bizonyítás. Indirekt módon tegyük fel, hogy létezik az algoritmus által megadott olyan legrövidebb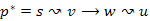 
út, hogy az i-dik lépésben az 
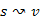részutat már ismerjük, de 
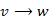él még nem része a fának, vagy 
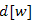értéke nem konzisztens, tehát mindkét esetben 
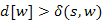, továbbá az i-dik lépésben nem történik változás. Azonban 
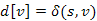és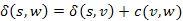 
, továbbá az i-dik lépésben a (v,w) él közelítése során 
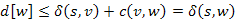, ami ellentmond az indirekt feltevésnek.
Ha a fenti gyorsítási lehetőséget beépítjük az algoritmusba, akkor az élek feldolgozási sorrendje befolyásolja az iterációk számát. Ha példánkban így átcímkéztük a csúcsokat: 5→1, 1→4, 2→3, 3→2, 4→5, és az élek feldolgozási sorrendje továbbra is csúcsok címkéje szerint rendezettséget követi, akkor egyetlen iterációs lépésben megkapjuk a megoldást. (Ezzel valójában az élek feldolgozási sorrendjét módosítottuk.)
 |
 |
 |
A tananyag az ELTE - PPKE informatika tananyagfejlesztési projekt (TÁMOP-4.1.2.A/1-11/1-2011-0052) keretében valósult meg.
A tananyag elkészítéséhez az ELTESCORM keretrendszert használtuk.