Az irányítás nélküli élsúlyozott gráfokon megfogalmazható feladat az, amely a csúcsokat összekötő minimális költségű fa (feszítőfa) megkeresését tűzi ki célul. Ez a feladat hasonlóan egyszerű és alapvetően fontos, mint az útkeresés, szintén komoly gyakorlati alkalmazásokkal a háttérben.
A probléma megjelenése egy időszakban, a villamosítás éveiben elég gyakori volt. Ha egy terület villamosítását kell megoldani a lehető legkisebb költséggel, akkor a feladat minimális összköltségű vezetékrendszer tervezése megadott helységek között.
A modellünk legyen irányítás nélküli, súlyozott gráf, ahol a városoknak megfeleltetjük a gráf pontjait, az éleknek pedig a tervezett, két várost összekötő villamos vezetéket. Az élek irányítás nélküliek az elektromos áram irányítatlan tulajdonsága miatt, és súlyozottak, ahol az élek költségei legyenek a becsült építési költségek.
Az itt következő egyetlen nagy fejezet – elméleti fogalmak rövid áttekintés után – három nagyobb egységből áll. A fejezet felépítése fordított sorrendet követ, mint az elmélet fejlődése. A feladat két ismert megoldásának, Prim, illetve Kruskal algoritmusának ismertetését megelőzi a piros-kék eljárás leírása, amely időben utoljára született.
Az előbb említett két megoldó algoritmus a probléma megoldására közvetlenül implementálható eljárásokat ad. Az általános és többszörösen nem-determinisztikus piros-kék algoritmus viszont inkább az elméleti megközelítés műfajába tartozik, ugyanis az eddig ismert megoldó eljárásokat mind magában foglalja lehetőségként.
Az általános eljárás és a két megoldó algoritmus ismertetését rövid bevezető jellegű, elméleti előkészítés előzi meg.
Definíciók:
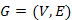 irányítatlan gráf. A
irányítatlan gráf. A 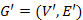 gráfot a
gráfot a 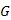 részgráfjának nevezzük, ha
részgráfjának nevezzük, ha 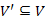 és
és 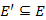 , továbbá
, továbbá 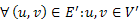 .
.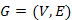 irányítatlan, összefüggő, véges gráf. A G egy körmentes, összefüggő
irányítatlan, összefüggő, véges gráf. A G egy körmentes, összefüggő 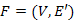 részgráfját a G egy feszítőfájának nevezzük. (A jelölésből látható, hogy
részgráfját a G egy feszítőfájának nevezzük. (A jelölésből látható, hogy  és
és 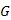 csúcsainak halmaza megegyezik.)
csúcsainak halmaza megegyezik.)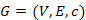 irányítatlan, összefüggő, élsúlyozott, véges gráf a
irányítatlan, összefüggő, élsúlyozott, véges gráf a 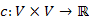 költségfüggvénnyel. Ekkor
költségfüggvénnyel. Ekkor 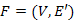 feszítőfa a
feszítőfa a 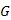 egy minimális költségű feszítőfája, ha költsége
egy minimális költségű feszítőfája, ha költsége  minimális a
minimális a 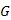 feszítőfái között, azaz
feszítőfái között, azaz 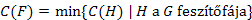 .
.Feladat: Adott egy 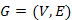 irányítatlan, összefüggő, élsúlyozott, véges gráf. Határozzuk meg
irányítatlan, összefüggő, élsúlyozott, véges gráf. Határozzuk meg 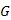 egy minimális költségű feszítőfáját.
egy minimális költségű feszítőfáját.
A továbbiakban tekintsünk néhány fákkal kapcsolatos tulajdonságot, amelyek a későbbi bizonyítások során hasznosak lehetnek.
Állítás: Minden legalább kétpontú fában van elsőfokú csúcs.
Bizonyítás: Tekintsük 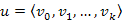 egyik leghosszabb utat a fában. Ha
egyik leghosszabb utat a fában. Ha 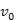 -ból menne él egy olyan csúcsba, amely nem eleme
-ból menne él egy olyan csúcsba, amely nem eleme 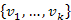 halmaznak, akkor
halmaznak, akkor 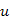 nem lenne a leghosszabb út, ha
nem lenne a leghosszabb út, ha 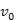 -ból menne él egy olyan csúcsba, amely eleme
-ból menne él egy olyan csúcsba, amely eleme 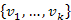 halmaznak, akkor az útban lenne kör, tehát nem lenne fa. Így azt kaptuk,
halmaznak, akkor az útban lenne kör, tehát nem lenne fa. Így azt kaptuk, 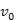 elsőfokú csúcs.
elsőfokú csúcs.
Állítás: Minden összefüggő 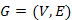 gráfnak van feszítőfája.
gráfnak van feszítőfája.
Bizonyítás: Ha a gráfban van kör, elhagyjuk az egyik élét. Ezt véges sokszor ismételve körmentes, összefüggő 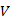 csúcshalmazú gráfot kapunk, tehát feszítőfát.
csúcshalmazú gráfot kapunk, tehát feszítőfát.
Állítás: Egy 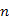 pontú összefüggő gráf fa akkor, és csak akkor, ha
pontú összefüggő gráf fa akkor, és csak akkor, ha 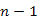 éle van.
éle van.
Bizonyítás:
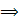 : Ha egy
: Ha egy 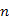 pontú fából törlünk egy elsőfokú csúcsot és a hozzá tartozó élt, akkor egy
pontú fából törlünk egy elsőfokú csúcsot és a hozzá tartozó élt, akkor egy 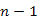 pontú fát kapunk. Ezt ismételve,
pontú fát kapunk. Ezt ismételve, 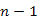 -szer lehet elsőfokú csúcsot elhagyni a hozzá tartozó éllel együtt, mivel a végén már csak egyetlen csúcs marad, tehát az eredeti fának n-1 éle volt.
-szer lehet elsőfokú csúcsot elhagyni a hozzá tartozó éllel együtt, mivel a végén már csak egyetlen csúcs marad, tehát az eredeti fának n-1 éle volt.
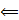 : Legyen
: Legyen  egy
egy 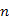 pontú,
pontú, 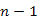 élű összefüggő gráf, továbbá legyen
élű összefüggő gráf, továbbá legyen egy feszítőfája
egy feszítőfája  -nek. Az előbb igazoltak szerint
-nek. Az előbb igazoltak szerint  -nek is
-nek is 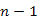 éle van, tehát
éle van, tehát 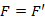 .
.
Állítás: Egy fa bármely két pontja között pontosan egy út vezet.
Bizonyítás: Indirekt tegyük fel, hogy 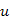 -ból
-ból 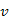 -be két út vezet, ekkor
-be két út vezet, ekkor 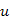 -ból
-ból 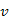 -be elmegyek az egyik úton, majd visszajövök a másik úton, akkor legkésőbb
-be elmegyek az egyik úton, majd visszajövök a másik úton, akkor legkésőbb 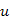 -ba jutva találok egy olyan csúcsot, amely eleme az első útnak, tehát kört találtam.
-ba jutva találok egy olyan csúcsot, amely eleme az első útnak, tehát kört találtam.
Állítás: Legyen 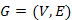 gráfnak
gráfnak 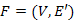 egy minimális költségű feszítőfája, továbbá, legyen
egy minimális költségű feszítőfája, továbbá, legyen 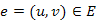 a
a 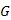 -nek egy olyan éle, ami nem éle
-nek egy olyan éle, ami nem éle  -nek (
-nek (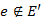 ). Tegyük fel, hogy az
). Tegyük fel, hogy az  -beli
-beli 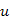 -ból
-ból 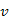 -be vezető úton van olyan
-be vezető úton van olyan 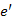 él (
él (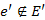 ), amelyre
), amelyre 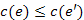 .
.  -ből az
-ből az  él hozzá vételével és az
él hozzá vételével és az 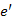 elhagyásával kapott
elhagyásával kapott  gráf is minimális költségű feszítőfája
gráf is minimális költségű feszítőfája 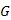 -nek.
-nek.
Bizonyítás: Vegyük hozzá  -hez
-hez  élt, ekkor a kapott gráfban van olyan kör, amelynek
élt, ekkor a kapott gráfban van olyan kör, amelynek 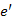 éle. Az
éle. Az 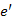 törlésével kapott gráf tehát összefüggő marad és éleinek a száma is ugyanannyi, mint F éleinek a száma, így
törlésével kapott gráf tehát összefüggő marad és éleinek a száma is ugyanannyi, mint F éleinek a száma, így  is feszítőfája
is feszítőfája 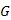 -nek. Továbbá
-nek. Továbbá 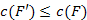 , mivel
, mivel 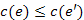 , azaz egy nem nagyobb költségű éllel cseréltünk le egy élt.
, azaz egy nem nagyobb költségű éllel cseréltünk le egy élt.
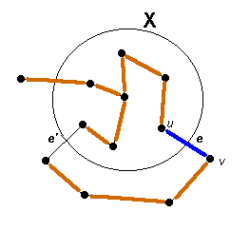
Szemléltessük az utolsó állítást a 27.1. ábrán. Legyenek 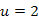 ,
, 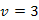 csúcsok, továbbá
csúcsok, továbbá 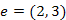 ,
, 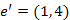 az állításban említett élek. Az állítás szerint, ha
az állításban említett élek. Az állítás szerint, ha 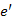 él helyett
él helyett  élt vesszük fel a feszítőfa éle közé, akkor áttérünk a
élt vesszük fel a feszítőfa éle közé, akkor áttérünk a 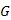 -nek egy másik minimális költségű feszítőfájára.
-nek egy másik minimális költségű feszítőfájára.
 fej27_s1_full.png27.1. ábra. Az élcsere hatása a feszítőfára
fej27_s1_full.png27.1. ábra. Az élcsere hatása a feszítőfáraA fejezetben tárgyalt algoritmusok közös vonása, hogy valamilyen módszer szerint sorra veszik a gráf éleit, és egyes éleket bevesznek a kialakuló minimális költségű feszítőfába, másokat pedig nem. Ezen algoritmusok általánosításaként Robert E. Tarjan adott egy szép, nem determinisztikus eljárást, melyet piros-kék eljárásként emlegetnek. A szemléletes tárgyalás érdekében az éleket szokás beszínezni, innen származik a módszer neve is.
A módszer kékre színezi a minimális költségű feszítőfába bekerülő élt, és pirosra színezi azokat az éleket, amelyek már biztosan nem kerülnek be a fába. Az élek színezése során két szabályt fogunk alkalmazni a piros szabályt és a kék szabályt. A két szabályt tetszőleges sorrendben és tetszőleges helyen alkalmazhatjuk, akár véletlenített módon.
A később ismertetésre kerülő algoritmusokat (Prim, Kruskal) tekinthetjük úgy is, mint a piros-kék eljárás egy-egy specializált változatait. Az algoritmus ismertetése előtt bevezetjük a szükséges definíciókat.
Definíciók:
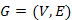 irányítatlan, súlyozott véges gráf éleinek egy színezését, amelynél egy él lehet piros, kék vagy színtelen. Ez a színezés megfelelő, ha létezik G-nek olyan minimális költségű feszítőfája, ami az összes kék élt tartalmazza, de egyetlen piros élt sem tartalmaz.
irányítatlan, súlyozott véges gráf éleinek egy színezését, amelynél egy él lehet piros, kék vagy színtelen. Ez a színezés megfelelő, ha létezik G-nek olyan minimális költségű feszítőfája, ami az összes kék élt tartalmazza, de egyetlen piros élt sem tartalmaz.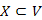 ,
, 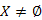 csúcshalmazt, amiből nem vezet ki kék él. Ezután egy legkisebb súlyú
csúcshalmazt, amiből nem vezet ki kék él. Ezután egy legkisebb súlyú 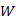 -ből kimenő színtelen élt fessünk kékre.
-ből kimenő színtelen élt fessünk kékre. 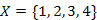 halmaz. Látható, hogy
halmaz. Látható, hogy 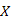 -ből nem vezet ki kék él. Színezzük kékre az
-ből nem vezet ki kék él. Színezzük kékre az 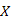 -ből "kivezető" egyik legkisebb súlyú élt, amely most a 3-as súlyú
-ből "kivezető" egyik legkisebb súlyú élt, amely most a 3-as súlyú 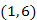 él.
él.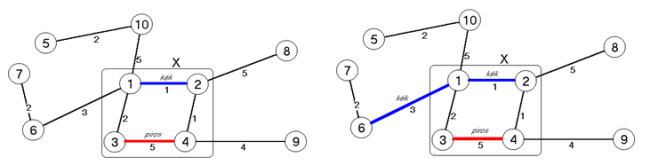 fej27_s2_full.png27.2. ábra. A kék szabály alkalmazása
fej27_s2_full.png27.2. ábra. A kék szabály alkalmazása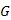 -ben egy olyan egyszerű kört, amiben nincs piros él. A kör egyik legnagyobb súlyú színtelen élét színezzük pirosra. A szabály egy alkalmazását illusztráljuk a 27.3. ábrán. A szabályban említett kör legyen
-ben egy olyan egyszerű kört, amiben nincs piros él. A kör egyik legnagyobb súlyú színtelen élét színezzük pirosra. A szabály egy alkalmazását illusztráljuk a 27.3. ábrán. A szabályban említett kör legyen  , amely nem tartalmaz piros élt. Keressük meg a kör egyik legnagyobb súlyú élét, amely az 5-ös súlyú
, amely nem tartalmaz piros élt. Keressük meg a kör egyik legnagyobb súlyú élét, amely az 5-ös súlyú  él. Színezzük pirosra.
él. Színezzük pirosra.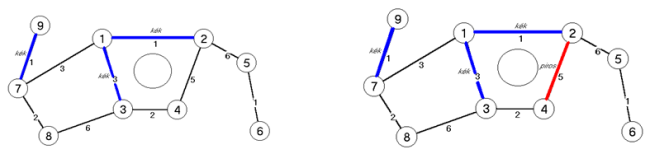 fej27_s3_full.png27.3. ábra. A piros szabály alkalmazása
fej27_s3_full.png27.3. ábra. A piros szabály alkalmazásaA fenti szabályok ismeretében a piros-kék eljárás könnyen megfogalmazható. Legyen kezdetben a 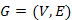 irányítatlan, súlyozott, összefüggő, véges gráf minden éle színtelen. Alkalmazzunk a két szabályt tetszőleges sorrendben és helyen, amíg csak lehetséges.
irányítatlan, súlyozott, összefüggő, véges gráf minden éle színtelen. Alkalmazzunk a két szabályt tetszőleges sorrendben és helyen, amíg csak lehetséges.
Állítás: Legyen 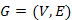 irányítatlan, súlyozott, összefüggő, véges gráf, és
irányítatlan, súlyozott, összefüggő, véges gráf, és 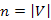 . Ekkor
. Ekkor
1.a piros-kék eljárás során a színezés mindig megfelelő marad;
2.a színezéssel sosem akadunk el, ameddig 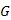 minden éle színes nem lesz;
minden éle színes nem lesz;
3.ha beszíneztük 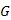 minden élét, akkor a kék élek
minden élét, akkor a kék élek 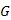 egy minimális költségű feszítőfájának éleit adják, sőt már
egy minimális költségű feszítőfájának éleit adják, sőt már 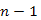 kékre színezett él után is megkaptuk az említett feszítőfát.
kékre színezett él után is megkaptuk az említett feszítőfát.
Bizonyítás:
 a
a 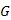 egy olyan minimális költség feszítőfája, amely az összes, jelenleg kékre színezett élt tartalmazza, és egyetlen, jelenleg pirosra színezett élt sem tartalmaz. Tegyük fel, hogy az eljárás következő lépése során az
egy olyan minimális költség feszítőfája, amely az összes, jelenleg kékre színezett élt tartalmazza, és egyetlen, jelenleg pirosra színezett élt sem tartalmaz. Tegyük fel, hogy az eljárás következő lépése során az 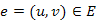 élt színeztük be. Két eset lehet attól függően, hogy melyik szabályt alkalmaztuk.
élt színeztük be. Két eset lehet attól függően, hogy melyik szabályt alkalmaztuk.a)Ha  éle
éle  -nek, akkor
-nek, akkor  mutatja, hogy megfelelő a színezés.
mutatja, hogy megfelelő a színezés.
b)Ha  nem éle
nem éle  -nek, akkor tekintsük az
-nek, akkor tekintsük az 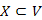 halmazt, amire a kék szabályt alkalmaztuk. Az
halmazt, amire a kék szabályt alkalmaztuk. Az  -ben
-ben 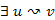 út, hiszen
út, hiszen  feszítőfa, továbbá ezen az úton van olyan
feszítőfa, továbbá ezen az úton van olyan 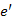 él, ami kimegy
él, ami kimegy  -ből. (Ugyanis
-ből. (Ugyanis  -t színeztük kékre, tehát a kék szabály értelmében
-t színeztük kékre, tehát a kék szabály értelmében  egyik vége
egyik vége 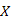 -en belül, a másik vége
-en belül, a másik vége  -en kívül van. Továbbá az említett
-en kívül van. Továbbá az említett 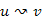
 -beli út, egy
-beli út, egy  -beli és egy
-beli és egy  -en kívüli pontot köt össze, tehát valahol ki kell lépnie
-en kívüli pontot köt össze, tehát valahol ki kell lépnie  -ből. Lásd 27.4. ábra.)
-ből. Lásd 27.4. ábra.)
 fej27_08_full.png27.5. ábra. Egy élcserével kialakított új feszítőfa (színesen jelölve)
fej27_08_full.png27.5. ábra. Egy élcserével kialakított új feszítőfa (színesen jelölve)Vizsgáljuk, milyen lehet 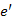 színe. Piros nem lehet, mivel része
színe. Piros nem lehet, mivel része  -nek, kék sem lehet, mivel a kék szabályt alkalmaztuk, amely szerint
-nek, kék sem lehet, mivel a kék szabályt alkalmaztuk, amely szerint  -nek olyannak kell lennie, amiből nem vezet ki kék él. Tehát
-nek olyannak kell lennie, amiből nem vezet ki kék él. Tehát 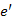 színtelen. Továbbá
színtelen. Továbbá 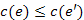 , mivel a kék szabály szerint az
, mivel a kék szabály szerint az  -ből kimenő egyik legkisebb súlyú élt kell választani, és mi
-ből kimenő egyik legkisebb súlyú élt kell választani, és mi  -t választottuk. Alkalmazhatjuk a korábbi állítást, mely szerint
-t választottuk. Alkalmazhatjuk a korábbi állítást, mely szerint  -ből
-ből 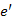 törlésével és
törlésével és  hozzá vételével kapott új
hozzá vételével kapott új  gráf is a
gráf is a 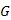 egy minimális költségű feszítőfája. Tehát
egy minimális költségű feszítőfája. Tehát  igazolja, hogy
igazolja, hogy  kékre színezésével a színezés továbbra is megfelelő marad (27.5. ábra).
kékre színezésével a színezés továbbra is megfelelő marad (27.5. ábra).
 fej27_08_full.png27.5. ábra. Egy élcserével kialakított új feszítőfa (színesen jelölve)
fej27_08_full.png27.5. ábra. Egy élcserével kialakított új feszítőfa (színesen jelölve) színe piros lett.
színe piros lett.a)Ha  nem éle
nem éle  -nek, akkor
-nek, akkor  mutatja, hogy megfelelő a színezés.
mutatja, hogy megfelelő a színezés.
b)Ha  éle
éle  -nek, akkor a pirosra színezés azt jelenti, hogy e továbbiakban már nem lehet éle az eljárás során előállítás alatt lévő minimális feszítőfának, tehát a megfelelő színezés bizonyításához át kell térni egy másik minimális feszítőfára. Az
-nek, akkor a pirosra színezés azt jelenti, hogy e továbbiakban már nem lehet éle az eljárás során előállítás alatt lévő minimális feszítőfának, tehát a megfelelő színezés bizonyításához át kell térni egy másik minimális feszítőfára. Az 
 -ből való törlésével
-ből való törlésével  két komponensre esik szét. Tekintsük azt a kört, amelyre a piros szabályt alkalmaztuk, ennek van olyan
két komponensre esik szét. Tekintsük azt a kört, amelyre a piros szabályt alkalmaztuk, ennek van olyan 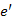 éle, amelyik a két komponenst összeköti és nem éle
éle, amelyik a két komponenst összeköti és nem éle  -nek. (Ugyanis a két komponenst összekötő e-től különböző élnek lennie kell, mivel kör mentén vizsgálódunk, és egy körbeli él elhagyásával az összefüggőség nem szűnhet meg. Továbbá, ha nem lenne ilyen
-nek. (Ugyanis a két komponenst összekötő e-től különböző élnek lennie kell, mivel kör mentén vizsgálódunk, és egy körbeli él elhagyásával az összefüggőség nem szűnhet meg. Továbbá, ha nem lenne ilyen 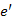 él, ami nem éle
él, ami nem éle  -nek, az azt jelenti, hogy a kör minden éle
-nek, az azt jelenti, hogy a kör minden éle  éle is, tehát kör lenne a fában. Lásd 27.6. ábra.)
éle is, tehát kör lenne a fában. Lásd 27.6. ábra.)
 fej27_s4_full.png27.6. ábra. Egy él elhagyásával keletkező két feszítőfa (színesen jelölve)
fej27_s4_full.png27.6. ábra. Egy él elhagyásával keletkező két feszítőfa (színesen jelölve)Vizsgáljuk, milyen lehet 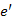 színe. Nem lehet kék, mivel nem éle
színe. Nem lehet kék, mivel nem éle  -nek és feltettük, hogy a színezés megfelelő, amit
-nek és feltettük, hogy a színezés megfelelő, amit  mutat. Nem lehet piros, mivel a piros szabály értelmében, olyan kört kell választani, amiben nincs piros él. Tehát
mutat. Nem lehet piros, mivel a piros szabály értelmében, olyan kört kell választani, amiben nincs piros él. Tehát 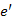 színtelen. Továbbá
színtelen. Továbbá 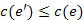 , mivel a piros szabály alkalmazása során e-t választottuk színezésre, amely szerint a kör egyik legnagyobb súlyú élét kell pirosra színezni. Az
, mivel a piros szabály alkalmazása során e-t választottuk színezésre, amely szerint a kör egyik legnagyobb súlyú élét kell pirosra színezni. Az 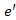 végpontjait összekötő
végpontjait összekötő  -beli út tartalmazza
-beli út tartalmazza  élt. (Ugyanis e törlése előtt
élt. (Ugyanis e törlése előtt  feszítőfa volt, és a korábbi állítás szerint, bármely két pontja között pontosan egy út vezet. Azonban most két olyan részre esett szét, amelynek egyik komponensében van
feszítőfa volt, és a korábbi állítás szerint, bármely két pontja között pontosan egy út vezet. Azonban most két olyan részre esett szét, amelynek egyik komponensében van 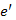 egyik vége, a másik komponensében
egyik vége, a másik komponensében 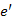 másik vége.
másik vége.  -ben a két komponens között az átjárást éppen az
-ben a két komponens között az átjárást éppen az  él biztosította, tehát az említett útnak át kell haladnia az
él biztosította, tehát az említett útnak át kell haladnia az  élen. Lásd 27.7. ábra.)
élen. Lásd 27.7. ábra.)
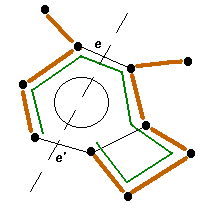 27.7. ábra. Az él két végpontját összekötő út (zölddel jelölve)
27.7. ábra. Az él két végpontját összekötő út (zölddel jelölve)Alkalmazhatjuk a korábban belátott állítást, mely szerint  -ből
-ből  törlésével és
törlésével és 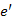 hozzá vételével kapott új
hozzá vételével kapott új  gráf is
gráf is 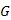 egy minimális költségű feszítőfája. Tehát
egy minimális költségű feszítőfája. Tehát  igazolja, hogy
igazolja, hogy  pirosra színezésével a színezés továbbra is megfelelő marad (27.8. ábra).
pirosra színezésével a színezés továbbra is megfelelő marad (27.8. ábra).
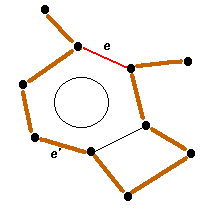 27.8. ábra. A kijelölt él pirosra színezésével kialakult új feszítőfa
27.8. ábra. A kijelölt él pirosra színezésével kialakult új feszítőfa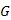 minden éle színes nem lesz. Tegyük fel, hogy
minden éle színes nem lesz. Tegyük fel, hogy 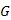 -nek még nem minden éle színes. Legyen
-nek még nem minden éle színes. Legyen  egy színtelen él. A színezés megfelelősége miatt a kék élek egy erdőt alkotnak (de lehet, hogy már egy fát, ekkor az alábbi 1. eset alkalmazható), az erdő fáit nevezzük kék fáknak. Két eset lehetséges:
egy színtelen él. A színezés megfelelősége miatt a kék élek egy erdőt alkotnak (de lehet, hogy már egy fát, ekkor az alábbi 1. eset alkalmazható), az erdő fáit nevezzük kék fáknak. Két eset lehetséges: két végpontja ugyanabban a kék fában van (27.9. ábra). Ekkor a piros szabályt alkalmazhatjuk arra a körre, aminek az éleit úgy kapjuk, hogy az e két végpontját összekötő egyetlen kék úthoz hozzávesszük
két végpontja ugyanabban a kék fában van (27.9. ábra). Ekkor a piros szabályt alkalmazhatjuk arra a körre, aminek az éleit úgy kapjuk, hogy az e két végpontját összekötő egyetlen kék úthoz hozzávesszük  -t.
-t.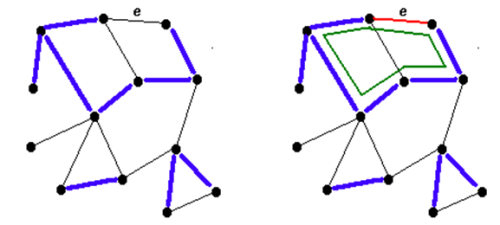 fej27_s5_full.png27.9.a ábra. Amennyiben az él két végpontja ugyanabban a fában van,
a piros szabályt alkalmazzuk (zölddel jelölve a kialakult kör)
fej27_s5_full.png27.9.a ábra. Amennyiben az él két végpontja ugyanabban a fában van,
a piros szabályt alkalmazzuk (zölddel jelölve a kialakult kör)
 legyen az egyik olyan kék fa csúcsainak halmaza, amelyikben benne van
legyen az egyik olyan kék fa csúcsainak halmaza, amelyikben benne van  egyik vége. Ebből a kék fából, azaz
egyik vége. Ebből a kék fából, azaz 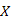 -ből biztosan megy ki él (legalább
-ből biztosan megy ki él (legalább  ), e kimenő élek közül az egyik legkisebb súlyú (nem biztos, hogy
), e kimenő élek közül az egyik legkisebb súlyú (nem biztos, hogy  ) kékre színezhető.
) kékre színezhető.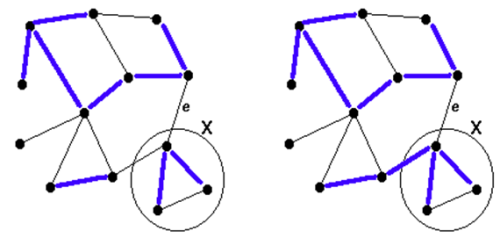 fej27_s6_full.png27.9.b ábra. Amennyiben az él két végpontja más fában van,
a kék szabályt alkalmazzuk
fej27_s6_full.png27.9.b ábra. Amennyiben az él két végpontja más fában van,
a kék szabályt alkalmazzuk
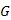 egy minimális költségű feszítőfáját. Ez rögtön következik abból, hogy a végső színezés is megfelelő. Az állítás második része szerint, az eljárást elegendő addig folytatni, míg
egy minimális költségű feszítőfáját. Ez rögtön következik abból, hogy a végső színezés is megfelelő. Az állítás második része szerint, az eljárást elegendő addig folytatni, míg 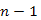 kék él nem lesz. A korábbi állítás szerint, a feszítőfának összesen
kék él nem lesz. A korábbi állítás szerint, a feszítőfának összesen 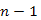 éle van, tehát ha már van
éle van, tehát ha már van 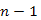 kék élünk, akkor a továbbiakban több nem is keletkezhet.
kék élünk, akkor a továbbiakban több nem is keletkezhet.Tehát a piros és kék szabályt tetszőleges helyen és sorrendben alkalmazva, végül minimális költségű feszítőfát kapunk, azonban hatékonysági szempontból megfontolandó melyik szabályt mikor és hol alkalmazzuk. A következő algoritmusokat a piros-kék eljárás egy-egy speciális esetének is tekinthetjük.
27.2. A Prim-algoritmus
A Prim algoritmus minden lépésben a kék szabályt alkalmazza egy s kezdőcsúcsból kiindulva. Az algoritmus működése során egyetlen kék fát tartunk nyilván, amely folyamatosan növekszik, míg végül minimális költségű feszítőfa nem lesz.
Kezdetben a kék fa egyetlen csúcsból áll, a kezdőcsúcsból, majd minden lépés során, a kék fát tekintve a kék szabályban szereplő  halmaznak, megkeressük az egyik legkisebb súlyú élt (mohó stratégia), amelynek egyik vége eleme a kék fának (
halmaznak, megkeressük az egyik legkisebb súlyú élt (mohó stratégia), amelynek egyik vége eleme a kék fának ( -ben van), a másik vége viszont nem (azaz nem eleme
-ben van), a másik vége viszont nem (azaz nem eleme  -nek). Az említett élt hozzá vesszük a kék fához, azaz az élt kékre színezzük, és az él
-nek). Az említett élt hozzá vesszük a kék fához, azaz az élt kékre színezzük, és az él  -en kívüli csúcsát hozzávesszük az X-hez.
-en kívüli csúcsát hozzávesszük az X-hez.
Az algoritmus megvalósításának a kulcsa az  -ből kimenő egyik legkisebb súlyú él meghatározása. Ehhez használjunk egy minimum választó elsőbbségi (prioritásos) sort (
-ből kimenő egyik legkisebb súlyú él meghatározása. Ehhez használjunk egy minimum választó elsőbbségi (prioritásos) sort (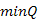 ), amelyben a fához még nem tartozó (még nem eleme
), amelyben a fához még nem tartozó (még nem eleme  -nek) csúcsokat tároljuk az
-nek) csúcsokat tároljuk az 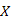 -től való távolsággal, mint kulcs értékkel. A távolság elnevezéséből adódóan és a korábbi algoritmusokhoz hasonlóan, jelöljük a kulcsot egy
-től való távolsággal, mint kulcs értékkel. A távolság elnevezéséből adódóan és a korábbi algoritmusokhoz hasonlóan, jelöljük a kulcsot egy 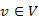 csúcs esetén
csúcs esetén 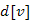 -vel.
-vel.
Egy 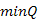 csúcs esetén az
csúcs esetén az  -től való távolság, azaz a
-től való távolság, azaz a 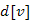 legyen azon élek közül a minimális súlyú él súlya, amely v és egy
legyen azon élek közül a minimális súlyú él súlya, amely v és egy 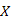 -beli csúcs között halad. Amennyiben nem létezik él v és egy tetszőleges
-beli csúcs között halad. Amennyiben nem létezik él v és egy tetszőleges  -beli csúcs között, legyen
-beli csúcs között, legyen 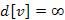 .
.
A korábbi algoritmusokhoz hasonlóan, a 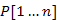 tömbbe tároljuk el egy csúcs feszítőfabeli megelőzőjét (szülőjét), amelynek segítségével bejárható a fa.
tömbbe tároljuk el egy csúcs feszítőfabeli megelőzőjét (szülőjét), amelynek segítségével bejárható a fa.
Az algoritmus elvénél, azt mondtuk, hogy kezdetben a kék fa legyen egyetlen pont, a kezdőcsúcs. Most az  -től való távolság fogalmának bevezetésével, azt mondhatjuk, hogy kezdetben
-től való távolság fogalmának bevezetésével, azt mondhatjuk, hogy kezdetben 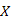 legyen az üres halmaz, amelytől a kezdőcsúcs nulla távolságra van, az összes többi csúcs pedig végtelen távolságra. Az algoritmus leírásában az
legyen az üres halmaz, amelytől a kezdőcsúcs nulla távolságra van, az összes többi csúcs pedig végtelen távolságra. Az algoritmus leírásában az 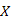 halmazt explicite nem ábrázoljuk, hanem
halmazt explicite nem ábrázoljuk, hanem 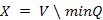 .
.
Az algoritmus minden lépésében kivesszük a 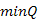 (egyik) legkisebb kulcsú elemét (az
(egyik) legkisebb kulcsú elemét (az 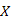 -ből kimenő egyik legkisebb súlyú él
-ből kimenő egyik legkisebb súlyú él  -en kívüli csúcsát), azaz a készülő feszítőfához, X-hez hozzávesszük az illető csúcsot. Majd az
-en kívüli csúcsát), azaz a készülő feszítőfához, X-hez hozzávesszük az illető csúcsot. Majd az  -en kívüli csúcsok
-en kívüli csúcsok  -től való távolságát, mint invariáns tulajdonságot karban kell tartani. Nyilván elegendő az
-től való távolságát, mint invariáns tulajdonságot karban kell tartani. Nyilván elegendő az  -be újonnan bekerült csúcs szomszédjainak az
-be újonnan bekerült csúcs szomszédjainak az  -től való távolságát módosítani (ha szükséges), mivel egy v csúcs úgy kerülhet közelebb
-től való távolságát módosítani (ha szükséges), mivel egy v csúcs úgy kerülhet közelebb  -hez, hogy valamelyik u szomszédja bekerül az
-hez, hogy valamelyik u szomszédja bekerül az  -be. Ekkor v távolsága a következőképpen alakul:
-be. Ekkor v távolsága a következőképpen alakul:
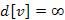 , akkor most legyen
, akkor most legyen 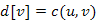 ;
;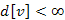 , akkor már létezik v-nek olyan w szomszédja, amely eleme
, akkor már létezik v-nek olyan w szomszédja, amely eleme  -nek tehát
-nek tehát 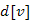 akkor változik, ha az
akkor változik, ha az 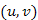 élen keresztül v közelebb van
élen keresztül v közelebb van  -hez, mint
-hez, mint 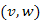 él esetén.
él esetén.Eközben a 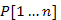 szülőségi tömböt is karban kell tartani.
szülőségi tömböt is karban kell tartani.
Tehát a használt típusok és adatszerkezetek:
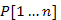 tömb: egy csúcs feszítőfabeli szülőcsúcsának a tárolására.
tömb: egy csúcs feszítőfabeli szülőcsúcsának a tárolására.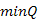 :
: 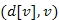 párokból álló minimumválasztó elsőbbségi sor, ahol
párokból álló minimumválasztó elsőbbségi sor, ahol 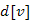 értéke a kulcs.
értéke a kulcs.Az algoritmus ADS szintű megvalósítása látható a 27.10. ábrán.
 fej27_17_full.png27.10. ábra. A Prim algoritmus és műveletigénye
fej27_17_full.png27.10. ábra. A Prim algoritmus és műveletigényeNézzük meg egy példán, ADS szinten az algoritmus működését a 27.10. ábrán. A szemléltetés érdekében színezzük a csúcsokat a következőképpen:
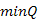 -nak és nincs
-nak és nincs 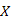 -beli szomszédja, azaz még nem került "látótávolságba", tehát az X-től való távolsága végtelen.
-beli szomszédja, azaz még nem került "látótávolságba", tehát az X-től való távolsága végtelen.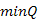 -nak, de létezik
-nak, de létezik 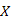 -beli szomszédja, tehát a távolsága már kisebb, mint végtelen.
-beli szomszédja, tehát a távolsága már kisebb, mint végtelen.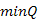 -ból, azaz bekerült
-ból, azaz bekerült 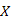 -be.
-be.A példában a kezdőcsúcs legyen az 1-es csúcs. Az inicializáló lépés után az 1-es csúcs kivételével minden csúcs távolsága (az  halmaztól) legyen végtelen, az 1-es csúcs távolsága pedig legyen 0, az
halmaztól) legyen végtelen, az 1-es csúcs távolsága pedig legyen 0, az  legyen az üres halmaz.
legyen az üres halmaz.
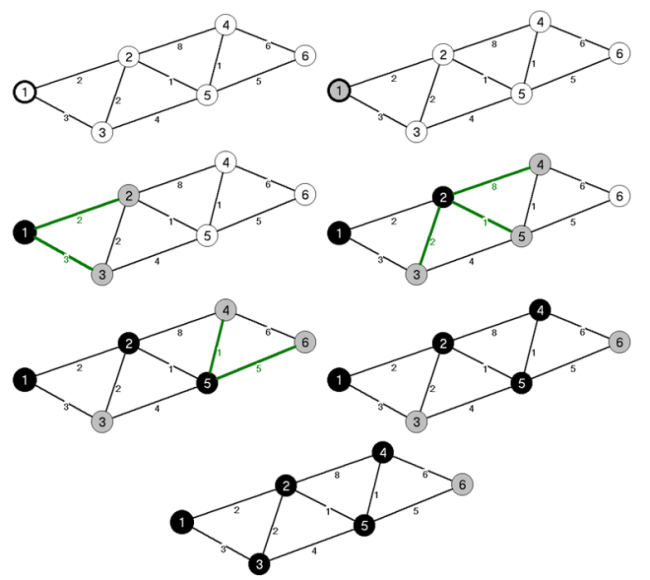 fej27_s7_full.png27.11. ábra. A Prim algoritmus lépésenkénti végrehajtása
fej27_s7_full.png27.11. ábra. A Prim algoritmus lépésenkénti végrehajtásaAz első lépésben kivesszük a 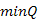 -ból az 1-es csúcsot (mivel az 1-es csúcs távolsága a legkisebb az
-ból az 1-es csúcsot (mivel az 1-es csúcs távolsága a legkisebb az  -től), tehát
-től), tehát 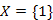 , majd az 1-es csúcs szomszédai (2 és 3) kerülnek közelebb az
, majd az 1-es csúcs szomszédai (2 és 3) kerülnek közelebb az  -hez. Ezek távolsága
-hez. Ezek távolsága 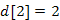 és
és 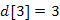 .
.
A második lépésben a 2-es csúcs kerül be az X halmazba (feljegyezve az 1-es csúcsot, mint fabeli szülőt), mivel közelebb van 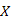 -hez, mint a 3-as csúcs. Ezután a 2-es szomszédai kerülnek "látótávolságba". Megfigyelhető, hogy a 3-as csúcs
-hez, mint a 3-as csúcs. Ezután a 2-es szomszédai kerülnek "látótávolságba". Megfigyelhető, hogy a 3-as csúcs 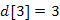 távolságra volt az X-től, de most közelebb került
távolságra volt az X-től, de most közelebb került 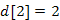 , a
, a 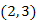 él figyelembe vételével,
él figyelembe vételével, 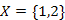 .
.
A harmadik lépésben az  halmazhoz a legközelebb lévő csúcs (
halmazhoz a legközelebb lévő csúcs (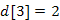 ,
, 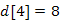 ,
, 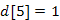 ), az 5-ös csúcs kerül az X halmazba (feljegyezve szülőként a 2-es csúcsot). Az 5-ös (még X-hez nem tartozó) szomszédai, a 4-es és 6-os csúcsok kerülnek közelebb az
), az 5-ös csúcs kerül az X halmazba (feljegyezve szülőként a 2-es csúcsot). Az 5-ös (még X-hez nem tartozó) szomszédai, a 4-es és 6-os csúcsok kerülnek közelebb az 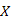 -hez.
-hez.
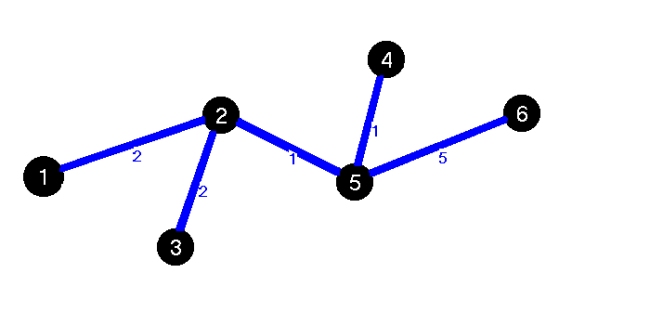
A negyedik lépésben a nem fekete csúcsok közül a legkisebb távolságú, a 4-es csúcs kerül az  -be.
-be.  . A 4-es szomszédai, a "4-esen keresztül" már nem kerülnek
. A 4-es szomszédai, a "4-esen keresztül" már nem kerülnek  -hez közelebb.
-hez közelebb.
Az ötödik lépésben a 3-as csúcs kerül az  -be. A 3-asnak már nincs is nem fekete (nem
-be. A 3-asnak már nincs is nem fekete (nem  -beli) szomszédja.
-beli) szomszédja.
Végül az utolsó lépésben a 6-os csúcs kerül az  halmazba. A menetközben feljegyzett szülőcsúcsok segítségével meghatározható a feszítőfa (27.12. ábra).
halmazba. A menetközben feljegyzett szülőcsúcsok segítségével meghatározható a feszítőfa (27.12. ábra).
 fej27_25_full.png27.12. ábra. A Prim algoritmus futtatása által kialakított feszítőfa
fej27_25_full.png27.12. ábra. A Prim algoritmus futtatása által kialakított feszítőfaVizsgáljuk meg a prioritásos sor (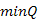 ) megvalósításának két, természetes módon adódó lehetőségét, ahogy a Dijkstra algoritmusnál is már láttuk:
) megvalósításának két, természetes módon adódó lehetőségét, ahogy a Dijkstra algoritmusnál is már láttuk:
1.A prioritásos sort valósítsuk meg rendezetlen tömbbel, azaz a prioritásos sor legyen maga a  tömb. Ekkor a minimum kiválasztására egy feltételes minimum keresést kell alkalmazni, amelynek a műveletigénye
tömb. Ekkor a minimum kiválasztására egy feltételes minimum keresést kell alkalmazni, amelynek a műveletigénye 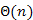 . A
. A 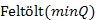 és a
és a 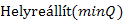 absztrakt műveletek megvalósítása pedig egy
absztrakt műveletek megvalósítása pedig egy  -pel történik.
-pel történik.
Az algoritmus ADT leírásában az szerepel, hogy a 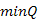 -ból kiveszünk egy elemet, azonban a
-ból kiveszünk egy elemet, azonban a 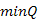 -t egy tömbbel valósítjuk meg, amelynek a mérete nem változik. Tehát osztályozni kell a csúcsokat aszerint, hogy a
-t egy tömbbel valósítjuk meg, amelynek a mérete nem változik. Tehát osztályozni kell a csúcsokat aszerint, hogy a 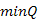 -ban vannak-e még, vagy már bekerültek az X halmazba. Legyen egy
-ban vannak-e még, vagy már bekerültek az X halmazba. Legyen egy 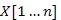 tömb az alábbi módon definiálva:
tömb az alábbi módon definiálva:
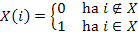
Az X tömböt kezdetben ki kell nullázni, majd menet közben karban kell tartani. Amint kikerül egy csúcs a 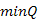 -ból, az X tömbben a csúcsnak megfelelő helyre 1-est kell írni.
-ból, az X tömbben a csúcsnak megfelelő helyre 1-est kell írni.
2.Kupac adatszerkezet használatával is reprezentálhatjuk a prioritásos sort. Ekkor a 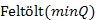 eljárás, egy kezdeti kupacot épít, amelynek a műveletigénye lineáris. Azonban most a
eljárás, egy kezdeti kupacot épít, amelynek a műveletigénye lineáris. Azonban most a  tömb változása esetén a kupacot is karban kell tartani, mivel a kulcs érték változik. Ezt a
tömb változása esetén a kupacot is karban kell tartani, mivel a kulcs érték változik. Ezt a 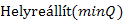 eljárás teszi meg, amely a csúcsot a gyökér felé "szivárogtatja" fel, ha szükséges (mivel a kulcs értékek csak csökkenhetnek). Ennek a műveletigénye
eljárás teszi meg, amely a csúcsot a gyökér felé "szivárogtatja" fel, ha szükséges (mivel a kulcs értékek csak csökkenhetnek). Ennek a műveletigénye 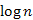 -es.
-es.
Ennél az ábrázolásnál is vezessünk be egy segédtömböt, a 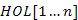 tömböt, amely megmutatja, hogy egy csúcs hol helyezkedik el a kupacban (a kupacot
tömböt, amely megmutatja, hogy egy csúcs hol helyezkedik el a kupacban (a kupacot 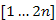 tömbben valósítsuk meg), illetve legyen 0, ha az illető csúcs már nem eleme a minQ-nak. A
tömbben valósítsuk meg), illetve legyen 0, ha az illető csúcs már nem eleme a minQ-nak. A 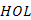 tömb felhasználásával egy csúcs prioritásos sorban való keresésének műveletigényét konstansra csökkenthetjük. A
tömb felhasználásával egy csúcs prioritásos sorban való keresésének műveletigényét konstansra csökkenthetjük. A 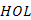 tömböt a
tömböt a 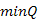 változásakor szintén karban kell tartani.
változásakor szintén karban kell tartani.
Megjegyzés: Nem szükséges kezdeti kupacot építeni, felesleges a kupacba rakni a végtelen távolságú elemeket. Kezdetben csak a kezdőcsúcs legyen a kupacban, majd amikor először elérünk egy csúcsot és a távolsága már nem végtelen, elég akkor berakni a kupacba.
A prioritásos sor fenti két megvalósítása esetén, a 27.10. ábrán láthatóan megfelelő módon alakul az algoritmus műveletigénye.
A belső ciklust célszerű globálisan kezelni, ekkor mondható, hogy összesen legfeljebb annyiszor fut le, ahány éle van a gráfnak.
3.Rendezetlen tömb esetén:
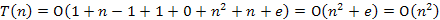
4.Kupac esetén:
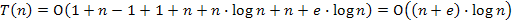
A Dijkstra algoritmusnál már említett következmény itt is érvényes, azaz sűrű gráf esetén csúcsmátrix és rendezetlen tömb, ritka gráf esetén éllista és kupac.
A Kruskal algoritmus mindkét szabályt alkalmazza a feszítőfa létrehozására, itt azonban egyértelmű él kiválasztási stratégiát alkalmazunk, amely meghatározza, mely szabályt kell alkalmaznunk.
Kezdetben legyen n db kék fa, azaz a gráf minden csúcsa egy-egy (egy pontból álló) kék fa, és legyen minden él színtelen. Minden lépés során kiválasztjuk az egyik legkisebb súlyú színtelen élt. Ha a kiválasztott él két végpontja különböző kék fában van, akkor színezzük kékre, különben (az él két vége azonos kék fában van, tehát a kék fa éleivel kört alkot) színezzük pirosra.
A fentiekből kitűnik, hogy a Kruskal algoritmust is tekinthetjük a piros-kék eljárás egy speciális esetének, ahol az élek színezésének a sorrendje egyfajta mohó stratégia szerint történik ("még mohóbb", mint a Prim algoritmusnál). Ugyanis
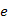 élt pirosra színezünk, akkor arra az egyszerű körre alkalmazható a piros szabály, amelynek élei az
élt pirosra színezünk, akkor arra az egyszerű körre alkalmazható a piros szabály, amelynek élei az 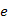 , és az
, és az 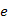 két végpontját összekötő kék út élei. Ez egy egyszerű kör, mivel pontosan egy
két végpontját összekötő kék út élei. Ez egy egyszerű kör, mivel pontosan egy 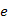 végpontjait összekötő kék út létezik, továbbá az
végpontjait összekötő kék út létezik, továbbá az 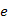 kivételével, minden éle kék, tehát
kivételével, minden éle kék, tehát 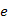 színezése előtt nem tartalmazott piros élt. Így teljesülnek a piros szabály feltételei.
színezése előtt nem tartalmazott piros élt. Így teljesülnek a piros szabály feltételei.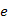 élt kékre színezünk, akkor e két kék fát köt össze,
élt kékre színezünk, akkor e két kék fát köt össze, 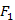 -et és
-et és  -őt. A kék fák definíciójából következik, hogy
-őt. A kék fák definíciójából következik, hogy 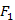 csúcsainak halmazából nem vezet ki kék él. Legyen
csúcsainak halmazából nem vezet ki kék él. Legyen 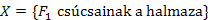 , ekkor az
, ekkor az 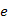 él lesz az egyik legkisebb súlyú X-ből kimenő színtelen él, mivel e az egyik legkisebb súlyú (nem csak X-ből kimenő) színtelen él. Tehát teljesülnek a kék szabály feltételei.
él lesz az egyik legkisebb súlyú X-ből kimenő színtelen él, mivel e az egyik legkisebb súlyú (nem csak X-ből kimenő) színtelen él. Tehát teljesülnek a kék szabály feltételei.Az algoritmus absztrakt szintjén, diszjunkt halmazokkal való műveleteket fogunk végezni. Tekintsük a kék fák csúcsainak (diszjunkt) halmazait (ezek a halmazok osztályozzák V-t). Amikor az egyik legkisebb súlyú színtelen élt kiválasztjuk, el kell dönteni, hogy a két végpontja azonos vagy különböző halmazban vannak-e. Majd a választól függően:
Az algoritmust akkor áll le, ha már nincs színtelen él (leállhatna már akkor is, ha az előbb következne be, hogy beszínezett 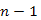 db kék élt). Mivel véges sok élünk van, és minden lépésben beszínezünk egyet, így
db kék élt). Mivel véges sok élünk van, és minden lépésben beszínezünk egyet, így  lépés után az algoritmus biztosan befejezi a működését.
lépés után az algoritmus biztosan befejezi a működését.
Az algoritmusban a következő absztrakt műveleteket szeretnénk használni:
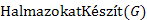 : Elkészíti a kezdeti n db, pontosan egy csúcsot tartalmazó diszjunkt halmazokat.
: Elkészíti a kezdeti n db, pontosan egy csúcsot tartalmazó diszjunkt halmazokat.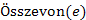 : Az e él két végpontja által reprezentált halmazokat összevonja.
: Az e él két végpontja által reprezentált halmazokat összevonja.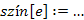 : Az e él színét változtatja meg az értékadás jobb oldalán szereplő színre.
: Az e él színét változtatja meg az értékadás jobb oldalán szereplő színre.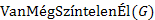 : igazat ad vissza, ha G-ben még van színtelen él, egyébként hamisat.
: igazat ad vissza, ha G-ben még van színtelen él, egyébként hamisat.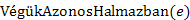 : igazat ad vissza, ha e két végpontja azonos halmazban van, egyébként hamisat.
: igazat ad vissza, ha e két végpontja azonos halmazban van, egyébként hamisat.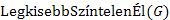 : Visszaadja a legkisebb súlyú színtelen élt.
: Visszaadja a legkisebb súlyú színtelen élt.Az algoritmus megvalósítása a 27.13. ábrán látható.
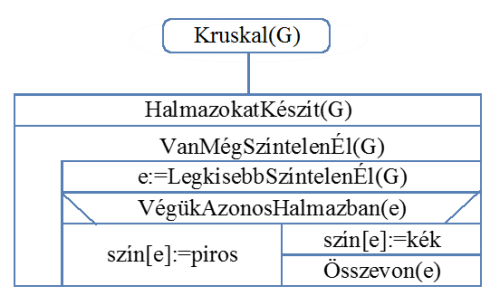 fej27_26_full.png27.13. ábra. A Kruskal algoritmus
fej27_26_full.png27.13. ábra. A Kruskal algoritmusA következő példában a csúcsok osztályokhoz (halmazokhoz/kék fához) való tartozását színezéssel illetve címkézéssel oldottuk meg. Az azonos színű csúcsok, azonos osztályba tartoznak. Tudjuk, hogy az osztályok reprezentálhatók egy-egy elemükkel, ezért az ábrán (a csúcs címkéje alatt), feltüntettük azon osztály egy reprezentáló elemének a címkéjét, amelyhez az illető csúcs tartozik. Tehát azok a csúcsok tartoznak egy osztályba (azonos kék fához), amelyeknél a címkéjük alatt megjelenő, méretét tekintve kisebb szám azonos.
Az inicializáló lépés után, minden él színtelen és minden csúcs külön osztályt alkot (27.13. ábra). Az első lépésben kiválasztjuk az egyik legkisebb súlyú élt, legyen ez 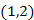 , és az 1-es ill. 2-es csúcsokat tartalmazó (egyelemű) halmazokat összevonjuk egyetlen
, és az 1-es ill. 2-es csúcsokat tartalmazó (egyelemű) halmazokat összevonjuk egyetlen 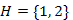 halmazzá. Az új halmaz reprezentáns eleme legyen az 1-es csúcs.
halmazzá. Az új halmaz reprezentáns eleme legyen az 1-es csúcs.
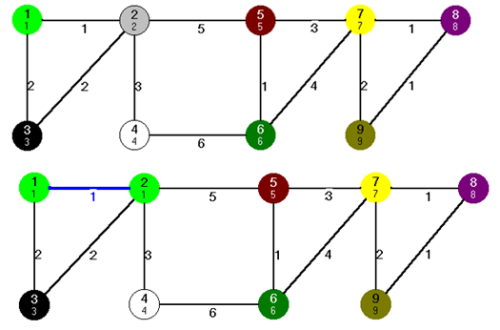 fej27_s8_full.png27.14. ábra. A Kruskal algoritmus inicializálása és első lépése
fej27_s8_full.png27.14. ábra. A Kruskal algoritmus inicializálása és első lépéseA következő lépésben, az első lépéshez hasonlóan járunk el az 5-ös és 6-os csúcsokkal. A harmadik lépésben, még mindig egyelemű halmazokat vonunk össze, most a 7-es és 8-as csúcsok osztályait. A negyedik lépésben a kiválasztásra kerülő  él, még mindig két különböző kék fát köt össze, így kékre kell színezni és a
él, még mindig két különböző kék fát köt össze, így kékre kell színezni és a 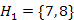 és
és 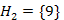 halmazokat össze kell vonni a
halmazokat össze kell vonni a 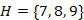 halmazzá. Az ötödik lépésben már nincs 1-es súlyú él. A következő egyik legkisebb súlyú él, valamelyik 2-es súlyú él lesz. Mi most válasszuk az
halmazzá. Az ötödik lépésben már nincs 1-es súlyú él. A következő egyik legkisebb súlyú él, valamelyik 2-es súlyú él lesz. Mi most válasszuk az 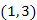 élt, amelyet kékre színezünk, és a végpontjainak megfelelő halmazokat összevonjuk. Eddig csak a kék szabályt alkalmaztuk, ahogy ez a 27.14. ábrán látható.
élt, amelyet kékre színezünk, és a végpontjainak megfelelő halmazokat összevonjuk. Eddig csak a kék szabályt alkalmaztuk, ahogy ez a 27.14. ábrán látható.
A hatodik lépésben kiválasztott 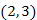 él két végpontja azonos kék fához tartozik, ezért színezzük pirosra (27.15. ábra). A hetedik lépésben ismét a piros szabályt alkalmazzuk, most a
él két végpontja azonos kék fához tartozik, ezért színezzük pirosra (27.15. ábra). A hetedik lépésben ismét a piros szabályt alkalmazzuk, most a  körre, amelynek következtében a
körre, amelynek következtében a  él piros lesz.
él piros lesz.
A nyolcadik lépésben a 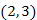 élt választjuk ki, és a kék szabályt alkalmazhatjuk az
élt választjuk ki, és a kék szabályt alkalmazhatjuk az 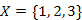 halmazra (27.16. ábra). Tehát a (2,4)-es élt kékre színezzük, aminek következtében azonos kék fába kerülnek az
halmazra (27.16. ábra). Tehát a (2,4)-es élt kékre színezzük, aminek következtében azonos kék fába kerülnek az 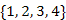 -es csúcsok. A Kruskal algoritmusnak megfelelően, a kék fák nyilvántartására, vonjuk össze őket egy halmazba. A kilencedik lépésben mindenképpen az
-es csúcsok. A Kruskal algoritmusnak megfelelően, a kék fák nyilvántartására, vonjuk össze őket egy halmazba. A kilencedik lépésben mindenképpen az 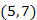 élt kell választanunk, mert ez az egyetlen 3-as súlyú színtelen él. Az élt színezzük kékre, és a
élt kell választanunk, mert ez az egyetlen 3-as súlyú színtelen él. Az élt színezzük kékre, és a 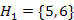 ,
, 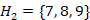 halmazokat vonjuk össze. A tízedik lépésben az egyetlen 4-es súlyú színtelen él kerül kiválasztásra, amelynek két végpontja azonos osztályba esik, ezért pirosra színezzük.
halmazokat vonjuk össze. A tízedik lépésben az egyetlen 4-es súlyú színtelen él kerül kiválasztásra, amelynek két végpontja azonos osztályba esik, ezért pirosra színezzük.
A tizenegyedik lépésben a 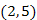 él a legkisebb súlyú színtelen él. Mivel a 2-es és 5-ös csúcsok különböző osztályokhoz tartoznak, így az élt színezzük kékre, és a
él a legkisebb súlyú színtelen él. Mivel a 2-es és 5-ös csúcsok különböző osztályokhoz tartoznak, így az élt színezzük kékre, és a 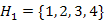 ,
, 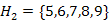 halmazokat vonjuk össze! A halmazok összevonása után már csak egy H={1,2,3,4,5,6,7,8,9} osztályunk (kék fánk) maradt. A továbbiakban már nem alkalmazhatjuk a kék szabályt, azaz megkaptunk egy minimális költségű feszítőfát, amelynek élei: (1,3),(1,2),(2,4),(2,5),(5,6),(5,7),(7,8),(8,9)
halmazokat vonjuk össze! A halmazok összevonása után már csak egy H={1,2,3,4,5,6,7,8,9} osztályunk (kék fánk) maradt. A továbbiakban már nem alkalmazhatjuk a kék szabályt, azaz megkaptunk egy minimális költségű feszítőfát, amelynek élei: (1,3),(1,2),(2,4),(2,5),(5,6),(5,7),(7,8),(8,9)
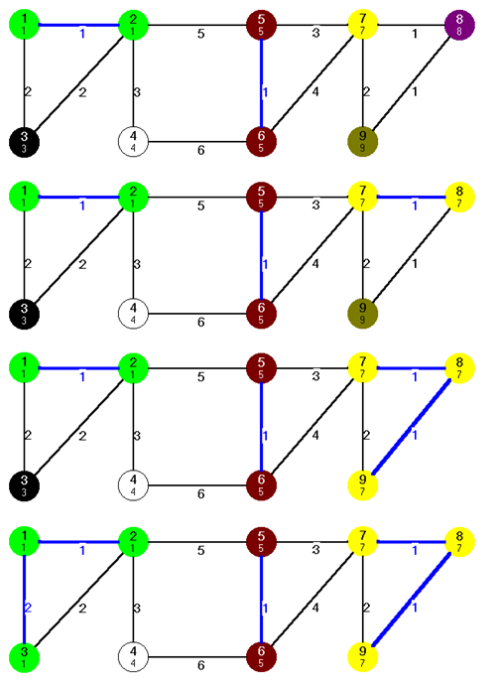 fej27_s9_full.png27.15. ábra. A kék szabály alkalmazásai
fej27_s9_full.png27.15. ábra. A kék szabály alkalmazásaiAz ADT szintű leírás szerint még maradt egy lépés, mivel még van egy színtelen él (4,6). Természetesen ezt az élt már csak pirosra színezhetjük (27.17. ábra).
Az ábrázolás szintjén nem tárgyaljuk az algoritmust. Jobban szemügyre véve a Kruskal algoritmust, a műveletigénye a diszjunkt halmazok megvalósításától függ. Amennyiben az éleket egy kupac adatszerkezetben tároljuk az élsúlyokkal, mint kulccsal, egy él kivétele 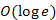 , e él kivétele
, e él kivétele 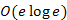 . Tehát jó lenne olyan ábrázolást választani a diszjunkt halmazoknak, hogy a teljes algoritmus műveletigénye
. Tehát jó lenne olyan ábrázolást választani a diszjunkt halmazoknak, hogy a teljes algoritmus műveletigénye 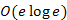 maradjon. Ilyen reprezentáció létezik; ez az UNIÓ-HOLVAN adatszerkezet (nem tárgyaljuk).
maradjon. Ilyen reprezentáció létezik; ez az UNIÓ-HOLVAN adatszerkezet (nem tárgyaljuk).
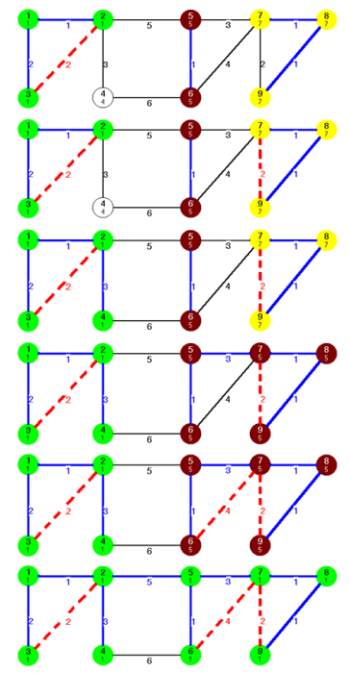 fej27_s10_full.png27.16. ábra. A feszítőfa kialakításának további lépései
fej27_s10_full.png27.16. ábra. A feszítőfa kialakításának további lépései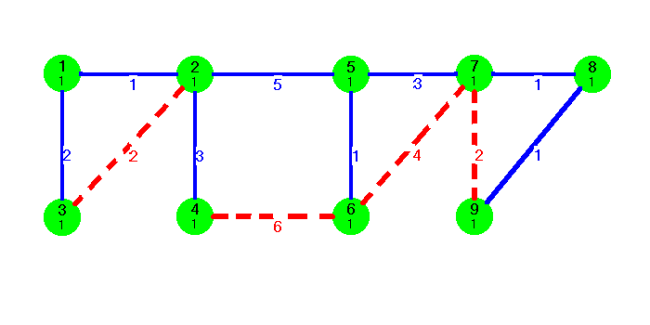 fej27_39_full.png27.17. ábra. A Kruskal algoritmus záró lépése
fej27_39_full.png27.17. ábra. A Kruskal algoritmus záró lépése |
 |
 |
A tananyag az ELTE - PPKE informatika tananyagfejlesztési projekt (TÁMOP-4.1.2.A/1-11/1-2011-0052) keretében valósult meg.
A tananyag elkészítéséhez az ELTESCORM keretrendszert használtuk.