34. A RABIN-KARP algoritmus

Az előző két mintaillesztő algoritmus a karakterekből álló minta minél nagyobb ugrásaival törekedett a szöveg illeszkedésre esélyes pozícióinak bejárására. Az előttünk álló Rabin-Karp eljárás a mintát, valamint a szöveg ugyanolyan hosszúságú szakaszait nagy egész számokkal kódolja, így az illeszkedés vizsgálat két szám egyenlőségének ellenőrzésére vezet.

Az eljárás ezzel a szemlélettel „elveszíti” a közvetlen kapcsolatot az egyes karakterekkel, így várhatóan nem lesz képes nagyobb ugrásokra, hanem mindig csak egy pozícióval csúsztatja jobbra a mintát a szövegen, ahol minden helyzet egy új egész számot határoz meg, mint a lefedett karakterek kódját. Tekinthetjük úgy az eljárást, hogy egy egész számokból álló sorozaton lineáris kereséssel keressünk egy szám első előfordulását, ahol ez a keresett szám a mintának a kódolásából származik.

Ettől a módszertől azt várhatjuk, hogy hatékony lesz, mivel az egész számokkal való műveletek gyorsan végrehajthatóak. Mivel azonban igen nagy számokról lehet szó, az egyelőségük fogalma és ellenőrzése összetettebb, mint a megszokott nagyságrendekben, így a hatékonyság nem magától értetődik.

34.1. Az algoritmus elvi alapjai

Legyen az ábécé a H véges halmaz, melynek elemeit sorszámozzuk meg 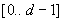közötti egész számokkal. Ekkor 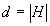, az ábécé betűinek száma. Ekkor egy H feletti szót (karakter sorozatot) úgy is tekinthetünk, mint egy d alapú számrendszerben felírt számot. Például a "BBAC" szónak megfelelő szám tízes számrendszerben 1102, ha az 'A', 'B' és 'C' sorszámai rendre 0, 1 és 2.

Vezessük be azt a függvényt, amely megadja egy karakter H-beli sorszámát: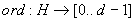

Ekkor az 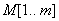mintának megfelelő szám

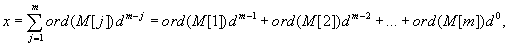
amelyet Horner algoritmussal hatékonyabban is kiszámíthatunk

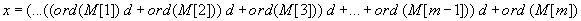
A Rabin-Karp algoritmus lényege az, hogy a bemutatott módon kapott x számot hasonlítjuk össze minden egyes k eltolás esetén, a szöveg részsorozatával, mint egy d alapú számrendszerben felírt számmal.

Jelöljük 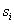-vel az 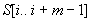szónak megfelelő számot (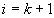). Ekkor a feladatot visszavezethetjük egy egész számok sorozatán való lineáris keresésre (lásd: 34.1. ábra).

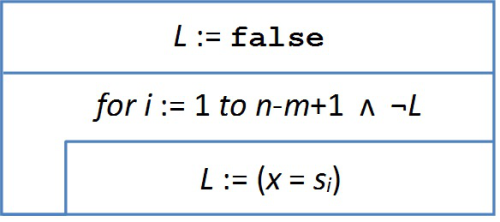A kép (nagyobb változata) külön ablakban is megtekinthető.fej33_524_full.png34.1. ábra. Lineáris keresés egész számok sorozatán

Nézzünk egy példát új eljárásunkra. Legyen a szöveg S="DACABBAC", a minta pedig M="BBAC". A 34.2. ábrán követhetjük, hogy az egyes pozíciókban milyen számok kerülnek összehasonlításra.

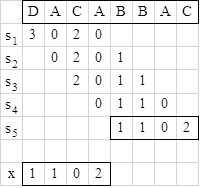A kép (nagyobb változata) külön ablakban is megtekinthető.34.2. ábra. Példa a lineáris keresés szerinti működésre

A példában az is látható, hogy a mintát kódoló x-et csak egyszer kell meghatározni (mivel nem változik). Azonban az s_i egész számokat minden léptetés után újra kell számolni, ami igen költséges még akkor is, ha Horner algoritmussal számítjuk. Hogyan lehetne s_i+1-et hatékony számolni s_iismeretében?

Legyen például a 23456 sorozat olyan, amelyben a 2345 szám nem egyezik a négy karakteres mintával. A 2345 szám ismeretében állítsuk elő a 3456 számot! Balról töröljük a 2-es számjegyet, majd a megmaradt 345 szám jegyeit egy helyi értékkel balra léptetjük, végül hozzáadjuk a 6-ot, azaz (2345-2*1000)*10+6=3456 lesz az új érték. Általánosan:

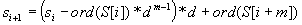
A formula két szorzást tartalmaz, mivel 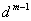-et előre kiszámíthatjuk, és egy változóban tárolhatjuk, így menet közben nem kell hatványozni.

A módszer lényegét körvonalaztuk, mivel egy karaktersorozat kölcsönösen egyértelműen megfeleltettünk egy egész számnak, a feladatot visszavezettük egy egész számokon értelmezett lineáris keresésre, amelynek műveletigénye a fenti formula használatával lineáris marad.

Vissza a tartalomjegyzékhez

34.2. Az algoritmus részletes kidolgozása

A gyakorlatban hosszabb minta vagy túl nagy ábécé esetén előfordulhat, hogy egy m számjegyből álló, d alapú számrendszerbeli szám nem tárolható egy szabványos egész számként (túlcsordul). Amennyiben nem egész számtípusként tároljuk, a műveletek végrehajtási ideje megnő.

A megoldás az, hogy vegyünk egy kellően nagy p prímet, amely mellett d*p még ábrázolható, és modulo p számoljuk az x-et és az s_i-t. Ekkor az egyértelműséget elveszítjük, mivel egyenlőség helyett a maradékosztályokhoz való tartozást vizsgáljuk, de ez a körülmény a nem-egyenlő eseteket nem teszi egyenlővé, azaz

(1)

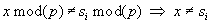
Ha viszont egyenlőséget állapít meg a vizsgálat, az csak azonos maradékosztályba való tartozást jelent, ami elvileg nem garantálja azt, hogy a két érték valóban egyenlő:

(2)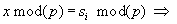 x és s_i azonos maradékosztályba esik, tehát további vizsgálat szükséges, azaz karakterenkénti összehasonlítással eldöntjük, hogy egyenlőség teljesül-e.

Hamis találatnak szokás nevezni azt az esetet, amikor 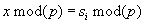, de . Minél nagyobb p-t választunk, a maradékosztályokba annál kevesebb elem esik, így várhatóan a hamis találatok száma is kevesebb lesz.

Visszatérve az s_i+1 érték számításának módjára, az most így módosul:

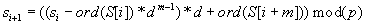
A modulo számítás következtében újabb probléma merült fel: 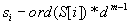értéke lehet negatív is, amely megkövetelné az előjeles egész számok használatát, így viszont abszolút értékben kisebb számok lennének ábrázolhatók, miközben p-t szeretnénk minél nagyobbnak választani. Adjunk ezért 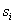-hez d*p-t, ami biztosítja, hogy a különbség nem lesz negatív, és az osztási maradékot sem változtatja:

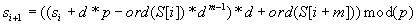
A kifejezés túlcsordulásának a megelőzésére számítsuk a kifejezést két lépésben (modulo esetén megtehetjük):

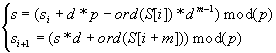
Összes eddigi megfontolásunkat tartalmazza a Rabin-Karp algoritmus végleges formája, amely a 34.3. ábrán látható.

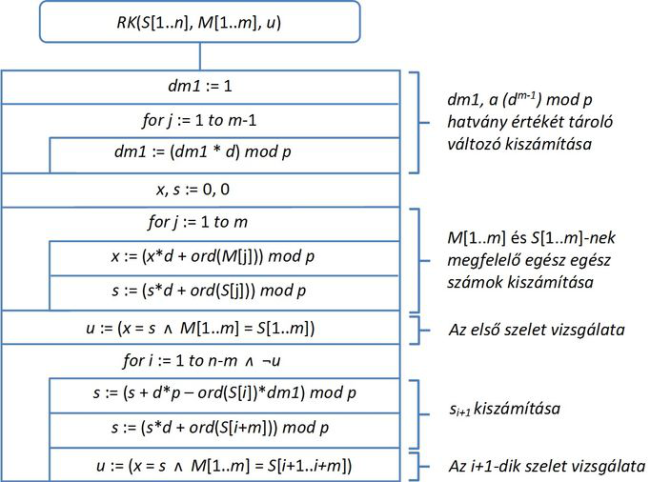A kép (nagyobb változata) külön ablakban is megtekinthető.fej33_540_full.png34.3. ábra. A Rabin-Karp algoritmus

A műveletigény a legjobb esete abból adódik, ha egyszerűen végigolvassuk a szöveget és minden esetben azt kapjuk, hogy a minta nem egyezik a lefedett szövegrésszel ().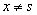

Ebben az esetben a mintaillesztés műveletigénye a szöveg hosszában lineáris lesz:

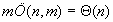
A legrosszabb eset akkor áll elő, ha a választott p prímszám mellett mindig hamis találatot kapunk. Ekkor minden esetben karakterenként is megvizsgáljuk az 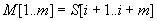egyenlőség teljesülését, Ebben az (elméletileg nem kizárható) esetben lényegében visszakapnánk az egyszerű mintaillesztés algoritmusát. Tehát

.

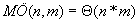A tapasztalat azt mutatja, hogy „jó” p választása esetén, nincs vagy csak nagyon kevés a hamis találat, így a Rabin-Karp algoritmus várhatóan lineáris marad:

.

A szekvenciális fájl input esetén fel kell készülni a puffer használatára, ugyanis az 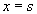találat esetén, a szövegben vissza kell lépni, és karakterenként meg kell vizsgálni az 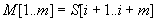egyenlőség teljesülését.

Vissza a tartalomjegyzékhez